Fundamental Concepts of Reservoir Geomechanics

23 minutes read

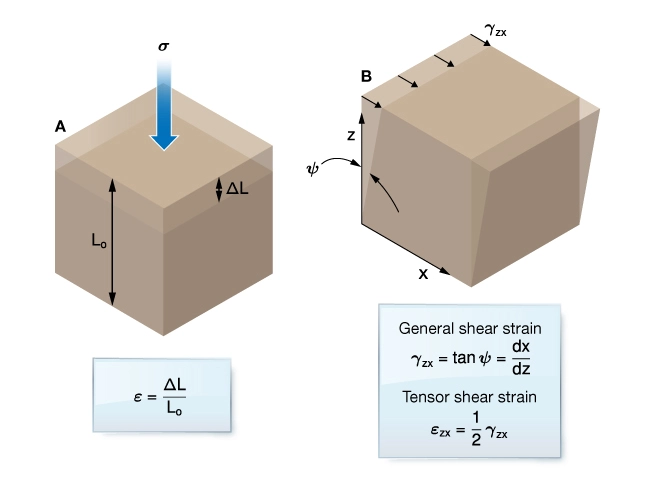
Strain

Strain is a continuum mechanics concept used to describe the deformation of a solid body. It is a measure of a rock’s response to stresses. Strain is measured in laboratory experiments to derive rock elastic parameters and strain terms are found in mathematical models of in-situ stress. Strain is a dimensionless quantity that can be thought of as the normalized displacement of points in a deforming material, $\Delta LL$ , where $\Delta L$ is the change in length of a reference line and $L$ is the initial length. Two general measures of strain are elongation and shear strain (Figure 1). Elongation $\varepsilon$ is defined as:

$\varepsilon = \dfrac{L - L_0}{L_0}$

Shear strain $\gamma$ is defined as:

$\gamma = \tan \psi$

$\gamma$ is also known as the engineering shear strain.

Measures of strain, Fundamental Concepts of Reservoir Geomechanics, Geomechanics — **Figure 1**: Measures of strain

Strain Tensor

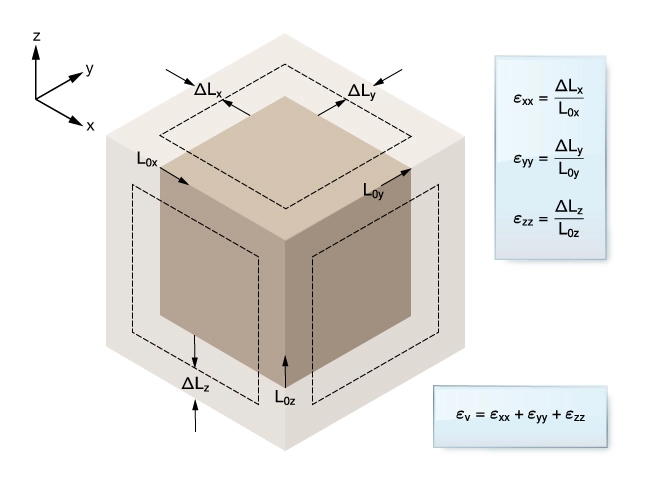
For conditions of infinitesimal strain, the deformation of a solid in three dimensions can be completely described by the six components of the second rank, or second direction, strain tensor. The six components are given by displacement gradients where u, v, and w are displacements relative to the rectangular coordinate axes x, y, z, respectively. The three normal strain components are defined as:

$\varepsilon _x = \dfrac{du}{dx}, \qquad \varepsilon _y = \dfrac{dv}{dy}, \qquad \varepsilon _z = \dfrac{dw}{dz}$

$\varepsilon _{xy} = \dfrac{1}{2}\left( \dfrac{dv}{dx} + \dfrac{du}{dy} \right), \qquad \varepsilon _{yz} = \dfrac{1}{2}\left( \dfrac{dw}{dy} + \dfrac{dv}{dz} \right), \qquad \varepsilon _{zx} = \dfrac{1}{2}\left( \dfrac{du}{dz} + \dfrac{dw}{dx} \right)$

Given these six quantities, the elongations and distortions of body can be calculated in any direction. These quantities are the components of the strain tensor $(\varepsilon _{ij})$ :

$\varepsilon _{ij} =\begin{bmatrix}\varepsilon _{xx} & \varepsilon _{xy} & \varepsilon _{xz} \\\varepsilon _{yx} & \varepsilon _{yy} & \varepsilon _{yz} \\\varepsilon _{zx} & \varepsilon _{zy} & \varepsilon _{zz} \end{bmatrix}$

Principal Strains

Principal strains are terms commonly found in elastic models of earth stress and in laboratory measurements of rock elastic moduli. As with the stress tensor, the strain tensor referred to principal coordinates contains only normal strain terms:

$\varepsilon _{ij} =\begin{bmatrix}\varepsilon _{xx} & 0 & 0 \\ 0 & \varepsilon _{yy} & 0 \\ 0 & 0 & \varepsilon _{zz} \end{bmatrix}$

Volumetric Strain

Volumetric strain $\varepsilon _v$ is a measure of the change in porosity of a rock. Volumetric strain is given by the trace of the strain tensor (Figure 2).

$\varepsilon _v = \varepsilon _{xx} +\varepsilon _{yy} +\varepsilon _{zz}$

Volumetric strain, Fundamental Concepts of Reservoir Geomechanics, Geomechanics — **Figure 2**: Volumetric strain

Infinitesimal Strain

The concept of infinitesimal strain is a fundamental approximation in the theory of linear elasticity and linear poroelasticity. The infinitesimal strain approximation is valid when strains are less than 10⁻³ to 10⁻². Practical examples include strains induced by the passage of elastic waves (10⁻⁸ to 10⁻⁷); tectonic strains (10⁻⁴ or less), and failure of high strength rocks (10⁻⁴ or less). However, weak rocks may not fail until strains reach one percent or more. Therefore, linear elasticity provides a reasonable approximation of rock deformation up to point of failure in all but the weakest rock materials.