Basin Formation Processes

Basin formation is a complex process that can be influenced by a variety of factors, including tectonic activity, sedimentation, and climate change.

Introduction to Basin Formation Processes

Basin Formation: Sedimentary basins form in response to tectonic processes, such as heating events and tectonic loading. These processes control the temporal and spatial evolution of subsidence. Changes in the shape of the basin as it subsides control the stratigraphic architecture, distribution of lithologies, structural styles and fluid-flow histories of the basin. Changes in the thermal regime of the basin control hydrocarbon maturation and, together with subsidence and fluid-flow histories, influence migration and diagenesis.

Although we can measure a variety of basin attributes, such as stratigraphic architecture, structural elements and maturation levels, we can not directly measure their evolution. We use process/response models of basin formation, or geodynamic models, to quantitatively estimate the subsidence and thermal histories from measurable basin properties.

Geodynamic models are mechanical or thermo-mechanical models that estimate the deformational response of the crust and lithosphere, or starting material, to applied forces, or loads. The weight of a sediment mass and subcrustal thermal density variations are both loads, although they have vastly different origins and cause different magnitudes and dimensions of deformation.

We call the mechanical properties and configuration of the lithosphere at the time of loading the initial conditions of our geodynamic model. The initial conditions of the lithosphere or crust influence its response to a load. For example, the lithosphere will deform differently in response to the same stress field if it is initially curved rather than flat.

Rheology

All basins form by thermal and/or mechanical tectonic loading of the lithosphere and are modified by the loads of sediment fill and changes in eustasy. The two primary controls on the magnitude, shape and rate of subsidence of a basin are the loading history (i.e., the magnitude, dimension and timing of tectonic, sediment and eustatic loads), and the mechanical properties and configurations of lithosphere that the loads deform.

Lithospheric deformation is a function of crustal and lithospheric thickness, temperature, composition and time. In general, the lithosphere becomes mechanically stronger with increasing thickness and decreasing temperature. Continental (felsic) lithosphere is stronger than oceanic (mafic) lithosphere. A primary control on basin subsidence is lithospheric-asthenospheric rheology. The rheology of a material describes the magnitude, shape and rate of deformation of that material when a load is applied. When discussing rheology, we often consider the following questions:

• When a load is applied, does the shape of the material remain constant or does it change? If the shape of the material remains constant, we call it a rigid solid.
• If the material changes shape, does it fracture, deform plastically or flow like a fluid?
• Does the material deform in different ways under different temperatures or over different durations of loading? A brittle material fractures, but the shape of the material between the fractures remains constant. An elastic material deforms but rebounds to its original shape when the load is removed. A plastic material deforms permanently and does not return to its original shape after the load is removed. A viscoelastic material bends like an elastic solid, but at the same time deforms by changing shape. If the material flows, it is a fluid.

The same material may also respond differently depending on the length of time a load is applied. For example, if we strike a windowpane with a hammer (high stress rate) at atmospheric temperature, it will behave like a brittle substance and shatter. If we gently push on a windowpane with a finger (moderate stress rate), it will behave elastically by bending and then rebounding when we remove our finger. Over decades (low stress rate), glass will flow like a fluid under its own weight (e.g., glass panes in old buildings are thicker at the base than at the top), or under the weight of material (e.g., centuries-old glass apothecary bottles containing mercury deform to flat-bottom flasks).

Temperature will also affect the response of a material to a load. With increasing temperature, glass subjected to a constant stress rate will change from a brittle or rigid solid, to a plastic, and finally to a molten fluid. Similarly, in the earth, rocks of asthenospheric composition are brittle at the earth’s surface, but behave like fluids when subjected to the temperatures and stress rates of the asthenosphere. The earth has layers of differing rheologies, and we use this layered structure to analyze responses to crustal loads on time scales of thousands to millions of years.

All thermal and mechanical basin-forming mechanisms tend toward isostatic equilibrium . Isostasy is the principle of hydrostatic balance between floating bodies due to the effect of buoyancy. Isostatic compensation is the principal mechanism for vertical movement of the lithosphere.

The response of the lithosphere to a load depends partly on the depth to which the stress from the load is transmitted. This depth depends on the depth of placement, magnitude and dimension of the load. For example, the load of an additional sand grain on the earth’s surface is not transmitted more than a few millimeters and causes no deformation because other grains can support the weight of a new grain. But a load the size of a mountain range causes lithospheric deformation because a mountain is sufficiently massive to transmit stress through the entire lithosphere and into the asthenosphere. Because the asthenosphere behaves like a fluid, it can buoyantly support the weight of a mountain or other crustal loads. A compensated load is one that is supported mechanically by the lithosphere and/or asthenosphere.

The fundamental assumption of isostasy is that large loads are supported by buoyancy forces within a deep fluid layer of the earth (Airy, 1855; Pratt, 1885). Because a fluid has no lateral strength it cannot support lateral pressure gradients; its pressure increases with depth, but the pressure is constant for each depth (Archimedes’ Principle). The total mass of each column of material above a constant depth in the fluid is constant (Figure 1, Isostatic compensation of column loads A through E.

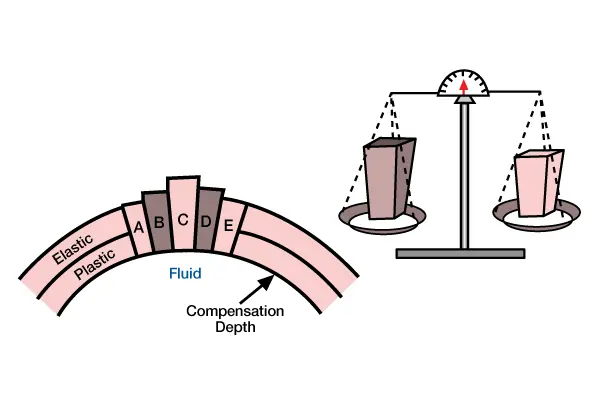
Loads are supported by bouyancy forces within the fluid atmosphere. Above a compensation depth within the fluid, each column load weighs an equal amount. The volumes of the columns differ because columns with less volume [less thivk and shaded darker] have higher average densities than columns with more volume [thicker and shaded lighter]. At depth of compression, pressure is constant, or isostatic.). We call this depth the depth of compensation . We consider a lithospheric load supported by buoyancy forces within the asthenosphere to be isostatically compensated.

The degree to which a load is isostatically compensated depends on the mass and dimension of the load and the duration over which it is applied. For example, individual fluvial point bars are not isostatically compensated, oceanic islands such as Hawaii are partially isostatically compensated, and continental shelves are fully isostatically compensated. Long-wavelength changes in elevation of the surface of the earth (e.g., continental shelves) are isostatically compensated by changes in thickness or average density of subjacent layers down to the depth of compensation.

There are two primary mechanisms of isostatic compensation for supporting loads — local and flexural compensation (Figure 2).

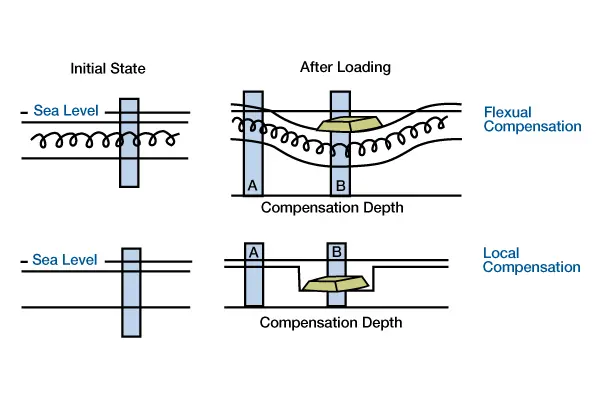
In local compensation, the loading response has sharp, distinct boundaries, whereas flexural compensation is a regional manifestation of isostasy, with the strata beyond the limits of the load also affected and involved in the compensation response. The amount of lithospheric deflection is the same for local and flexural compensation, but in flexure the deflection is distributed regionally. We can mathematically model this deflection to estimate deflections due to loading.

As we see in Figure 2, flexural compensation occurs where layers within the lithosphere have sufficient lateral strength to support the load, as if the layers were connected by springs. The load depresses the lithosphere beneath and adjacent to the load. Columns above a compensation depth (A and B) will not have equal weights because the load is partially supported by the lateral strength of the lithosphere. In local compensation, layers within the lithosphere have no lateral strength (no springs) to support the load. The load depresses the lithosphere only at the position of the load, as if the columns at the position of the load have Teflon-coated sides. Columns above a compensation depth will have equal weights because the load is supported entirely by buoyancy forces within the asthenosphere.

If a load is partially supported by the lateral strength of the lithosphere, the load will be partially isostatically compensated. Consequently, the vertical masses above a compensation depth will not be constant. We can use this property to measure degrees of compensation. We use rheological models to determine the time-varying values for lateral strength, which we use to develop basin deformation histories.