Hydraulic Fracturing Fundamentals
Rock Mechanical Properties and Fracturing
Certain formation properties are known to influence a fracture’s growth pattern. All of these properties must be measured or estimated for use as inputs into hydraulic fracturing models, which are used to design fracturing treatments and optimize fractured well performance.
Rock Mechanical Properties
Young’s Modulus
A rock’s elastic properties are most often described by Young’s modulus and Poisson’s ratio. Young’s modulus is essentially an index of the rock’s resistance to external force. It is defined as the ratio of an applied uniaxial stress to the resulting strain (Figure 1).
Where
E= young’s modulus
σ= uniaxial applied stress (applied force divided by cross-sectional area)
ε= strain (change in length divided by the original length)
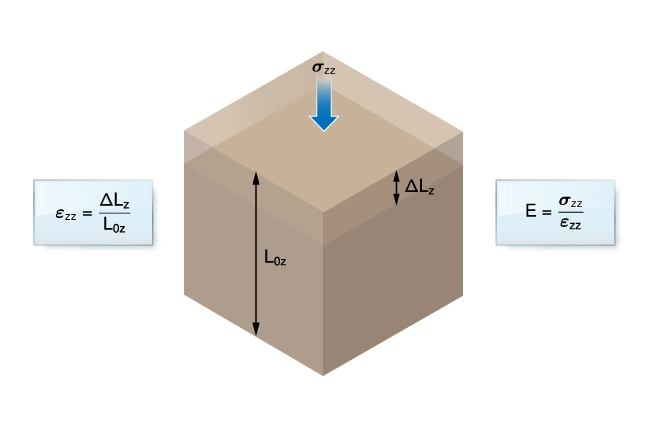
Figure 1: Body subjected to a uniaxial stress in the z-direction (σzz) illustrating the definition of Young’s modulus
Young’s modulus has the same dimensions as pressure, and is typically measured in units of pascals (Pa) or pounds per square inch (psi). Its value can be determined from a uniaxial stress test, in which a cylindrical sample of rock of known dimensions is subjected to a compressive force and the change in length and diameter is recorded. The applied stress divided by the resulting strain is Young’s modulus (E).
Young’s modulus is a function of lithology, porosity, fluid type, and other variables. Soft formations are characterized by E values as low as 105psi, while hard formations can have E values as large as 107psi (hard limestone).
Table 1 lists some typical values for Young’s modulus for various lithologies.
| Lithology | Young’s Modulus, psi |
|---|---|
| Soft sandstone | 0.1 to 1 x 106 |
| Medium sandstone | 2 to 5 x 106 |
| Hard sandstone | 6 to 10 x 106 |
| Limestone | 8 to 12 x 106 |
| Coal | 0.1 to 1 x 106 |
| Shale | 1 to 10 x 106 |
Higher values of Young’s modulus indicate greater stiffness. Therefore, a given amount of fracturing fluid will create a relatively long, narrow fracture in a rock having a high Young’s modulus value. The same amount of fluid will create a shorter but wider fracture in a rock with a low Young’s modulus value, provided all other properties are the same. This is one of the main differences in fracturing hard versus soft formations. If the Young’s modulus varies from layer to layer, it might cause a complex width profile, with reduced widths in the layers with higher modulus values.
Poisson’s Ratio
Poisson’s ratio is the ratio of the lateral strain demonstrated by a rock when subjected to a longitudinal load, divided by the amount of longitudinal strain caused by the same loading (Figure 2).
Where
Poisson’s ratio
uniaxial applied stress (applied force divided by cross-sectional area)
lateral strain
longitudinal strain
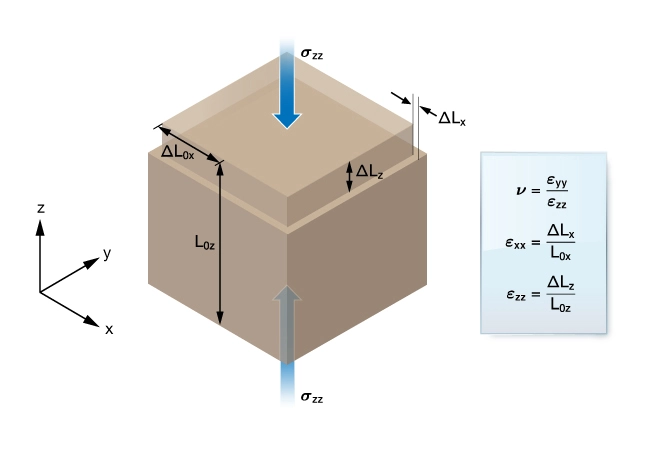
Poisson’s ratio is a dimensionless quantity, usually ranging from 0.10 to 0.45 (Table 2). It can also be measured in the laboratory via a uniaxial stress test. From a hydraulic fracturing standpoint, Poisson’s ratio is primarily responsible for translating vertical stress into horizontal stress. It also has some limited influence on fracture width.
| Lithology | Poisson’s ratio |
|---|---|
| Soft sandstone | 0.20 – 0.35 |
| Medium sandstone | 0.15 – 0.25 |
| Hard sandstone | 0.10 – 0.15 |
| Limestone | 0.30 -0.35 |
| Coal | 0.35 -0.45 |
| Shale | 0.28 – 0.43 |
It is important to understand that Young’s modulus and Poisson’s ratio are related to the elastic behavior of the rock. They can be measured on a core sample using “static” or “dynamic” measurement methods, or in-situ, using dynamic (mostly sonic) methods. The static and dynamic measurements may be somewhat different.
Plane Strain Modulus and Shear Modulus
The Plane Strain modulus (E′) is and the Shear Modulus (G) combine Young’s modulus and Poisson’s ratio: The plane strain modulus is numerically very near to the Young’s modulus, because the square of the Poisson’s ratio can usually be neglected with respect to one.
Tensile Strength
Tensile stress is the maximum stress that a material can tolerate without rupture in a uniaxial tensile experiment. Though the effect of the tensile strength is minimal during fracture extension, it affects the fracture initiation pressure. Tensile strength is an input parameter for hydraulic fracturing models. Its values, however, depend on the test method employed.
Fracture Toughness
The critical value of the stress intensity factor, or fracture toughness, characterizes a rock’s resistance to the propagation of an existing fracture. It is measured in units of pressure times the square root of length because the stress intensity factor at the tip of a fracture is the product of the pressure loading and the square root of a characteristic length (such as fracture half-length). Fracture propagation occurs when the stress intensity factor reaches its critical value. It is easier to propagate a larger fracture than a smaller one, provided the pressure loading on the fracture faces is the same.
When the stress intensity factor at the tip equals the fracture toughness, a special equilibrium state is reached. Vertical fracture extension or fracture height growth is often considered as a process passing through such an equilibrium state. Sometimes the lateral extension of the fracture is also considered as a sequence of such equilibrium states. The concept itself is important, but the actual value has limited effect on calculations. Laboratory measurements indicate fracture toughness values ranging from 500 to 2000 MPa-m0.5. Almost the same limits are obtained if the values are expressed in units of psi-inch0.5.
Permeability
The higher a formation’s matrix permeability, the higher the rate at which fluid leaks off into the formation. And the higher the fluid leakoff rate, the less driving force is available for fracture growth. Formation permeability is one of the main factors controlling fluid leakoff, and hence, indirectly affects fracture propagation. Porosity and total formation compressibility have a limited influence on fluid leakoff as well.
Poroelastic Constant
The poroelastic constant (α) is the bulk modulus of a dry rock sample divided by the same measurement in a fluid-saturated sample, where bulk modulus is the ratio of hydrostatic pressure to volumetric strain.
Where
bulk modulus of dry rock sample
bulk modulus of saturated sample
The saturated sample is more resistive to compression because the fluid carries part of the load. Therefore, the poroelastic constant is less than one. Most fracturing calculations assume an α value of between 0.7 and 1.
Formation Brittleness
If a material breaks easily without significant deformation or strain when subjected to stress, it is considered brittle. This characteristic is desirable in a formation that is to be hydraulically fractured. Particularly in the case of tight formations (e.g., shales) with variations in mineralogy, the objective would be to place hydraulic fractures in the most brittle portions of the formation in an effort to maximize permeability improvement. Consequently, methods have been developed to quantify the degree of brittleness in a given zone.
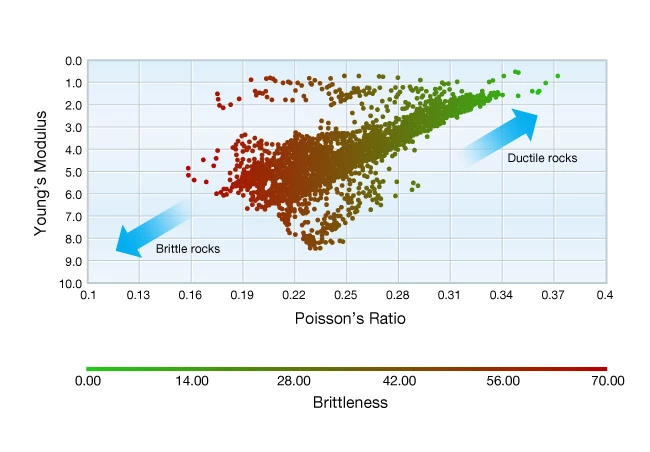
Rickman et al. (2008) suggested that a brittleness index can be computed from Poisson’s ratio and Young’s modulus. This approach is based on the notion that a low Poisson’s ratio reflects the rock’s ability to fail under stress and a high Young’s modulus reflects the rock’s ability to maintain a fracture once the rock fractures. The method proposes that a reservoir rock’s relative “frackability” can be determined from these factors, which may be measured or inferred from geophysical log measurements and used to guide hydraulic fracturing designs (Figure 3). This approach has proven useful but this brittleness index provides information only in a relative sense. Also, there are other elastic moduli besides Poisson’s ratio and Young’s modulus that can influence the rock’s fracturing tendencies, as can the porosity and relative mineral fractions (Cho and Perez, 2014).
