Introduction to Well Cementing

20 minutes read

Fluid Density

Density is a measure of mass per unit volume. In oilfield units, the density of fluids used in drilling, completion, and workover operations is loosely defined in weight per unit volume ( $\left( \tfrac{lb_w}{ft^3} = \tfrac{lb_m}{ft^3}\times g \right)$ ) , of $\tfrac{lb_w}{ft^3}$ or, more commonly, $\tfrac{lbm}{gal}$ (“ppg”).

Note: The mass of an object is a measure of the object’s inertial property, or the amount of matter it contains. The weight of an object is a measure of the force exerted on the object by gravity, or the force needed to support it. In everyday industry use, the term “weight” is often used as a synonym for “mass.” When used in this learning program, the term “weight” means “mass”.

Density Examples

Fresh Water

Fresh water has a density of 62.4 $\tfrac{lb_w}{ft^3}$ ( $\left( 1 \tfrac{kg}{l} = 1 \tfrac{g}{cm^3} \right)$ ) and $1\ ft^3 = 7.48\ US\ gallons$ .

Density (ppg) = Density $\tfrac{ \left(\tfrac{lb_m}{ft^3} \right)}{7.48}$
Density of water = 62.47.48=8.33 ppg

Conversely:

Density $\left( \tfrac{lb_m}{ft^3} \right) = 7.48 \times$ Density (ppg)
Density of water $= 7.48 \times 8.33 = 62.4 \tfrac{lb_m}{ft^3}$

Salt Water

The presence of salt in water increases its density. Salt water density varies according to its dissolved solids content, but typical seawater density is approximately 8.9 to 9.0 ppg. The average value is usually defined as 8.95 ppg.

Cement Slurry

The densities of neat cement slurries used in well construction and intervention range from 15.6 to 16.4 ppg, but can be increased to as high as 22 ppg when mixed with weighting additives.

Class A neat cement slurry density = 15.6 ppg

The Subsurface Pressure-Fluid Density Relationship: A Key Aspect of Well Operations

Pressure is the force exerted on a unit area. It can be expressed using any number of units (bar, atmospheres, psi, psf, kPa). Atmospheric pressure at standard conditions, for example, may be expressed as:

1 atmosphere (atm)
14.696 $\tfrac{lb_f}{in^2}$ (psi)
2116.224 $\tfrac{lb_f}{ft^2}$ (psf)
101.325 kPa (note: 1 bar = 100 kPa = 0.987 atm)

The oilfield unit most commonly used in well operations is pounds per square inch ( $\tfrac{lb_f}{in^2}$ , or psi).

In cementing operations it is necessary to understand the impact of fluid density on the pressure at depth in a wellbore.

Pressure Example

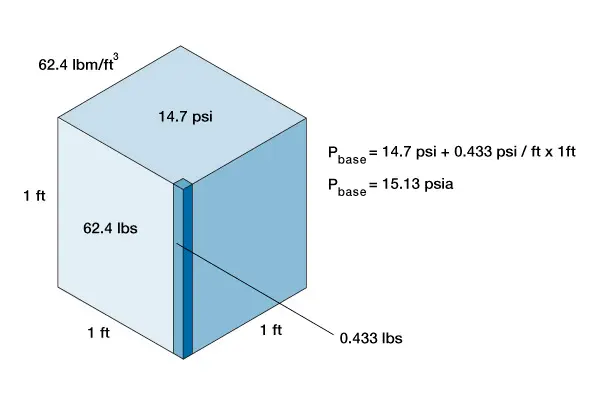
Fluid Density, Pressure at the base of a fresh water, Subsurface Pressure-Fluid Density Relationship — **Figure 1**: Pressure at the base of a fresh water-filled container (1 ft³)

For example, a cubic foot of water placed in a 1 ft × 1 ft × 1 ft container (Figure 1) weighs 62.4 lbs. Its base is 12 inches × 12 inches or 144 in², which means that each foot of water above a square inch weighs 0.433 lbs and the pressure at the base equals the pressure at the surface, atmospheric pressure, 14.7 psi, plus 0.433 psi. The pressure at the base of a fresh water-filled casing of height “h” is given by the relationship:

$P (psi) = 14.7\, (psi) + \dfrac{\textrm{fluid density }\left( \tfrac{lb_m}{ft^3} \right)}{144 \left( \tfrac{in^2}{ft^2} \right)}\times h(ft)$

The pressure 100 feet down a wellbore filled with fresh water will be equal to:

$P = 14.7\, psi + \dfrac{62.4}{144}\tfrac{psi}{ft}\times h(ft)$

$= 14.7 + 0.433 \times h$

$= 14.7 + 0.433 \times 100 = 58\ psia$

The rate of increase in pressure, 0.433 $\tfrac{psi}{ft}$ , is called the hydrostatic pressure gradient for fresh water.

If the density of the fluid is referred to as ppg ( $\tfrac{lbs}{gal}$ ) units then the relationship changes to:

$P = 14.7\, psi + \dfrac{\textrm{fluid density }(ppg)\times 7.48\tfrac{gal}{ft^3}}{144 \left( \tfrac{in^2}{ft^2} \right)}\times h(ft)$

$P = 14.7\, psi + 0.052 \tfrac{gal}{ft\times in^2}\times \textrm{fluid density} (ppg) \times h\, (ft)$

Using this equation, the pressure gradient of water, with a density of 8.33 ppg, is 0.433 $\tfrac{psi}{ft}$ .

Note that in many cementing calculations where pressure values are often very high, the addition of the atmospheric pressure term, 14.7 psi, is usually disregarded.

As illustrated in Figure 6, the bottomhole pressure depends on the vertical depth of a well whether it is drilled vertically or deviated to a point quite different from its vertical location.