Seismic Interpretation | What is seismic interpretation?

Where to Time

In discussing the basics of interpretation, we initially follow the practice of timing at regular intervals of reflection time; in fact, we select the timing at the contour interval. This is done for simplicity of explanation, because it eliminates the need to discuss the interpolation (sampling) of time values.

In fact, the normal practice of interpreters is to time the picked reflection at a regular progression of shotpoints, rather than at a regular progression of times, and then to interpolate the contour times between the timed shotpoints.

The problem of faithfully recording a continuous variation (such as reflection time along a line) by a series of discrete measurements made at regular intervals is the process called sampling. This process is subject to the sampling theorem. It makes no difference whether we sample at regular intervals of shotpoints or at regular intervals of time, provided that the measurements are made at appropriate intervals. Thus a long and simple monocline can be specified by just two widely-spaced measurements, but a rough eroded surface requires at least two measurements per cycle of the corrugation. Further, according to sampling theory, an additional step (reconstitution) is necessary before values can be interpolated between the measured values.

The reasonability of the sampling theorem is illustrated in Figure 1. In image A, we see an anticline whose crest has collapsed (blue line) because of irregular extensional faulting. The black dots are the time values corresponding to a regular progression of shotpoints across the anticline. The increment of the progression of shotpoints is too coarse because, when we post and contour these values, the structure appears as shown by the dashed green line, and all memory of the collapsed crest has disappeared. In image B we see a major high, a second high, and a small saddle between them. The time values are again represented by the black dots, the shotpoint values corresponding to regular intervals of reflection time. Again, the interval is too coarse because when we post and contour these values, it is not possible to determine whether the high is a single or double.

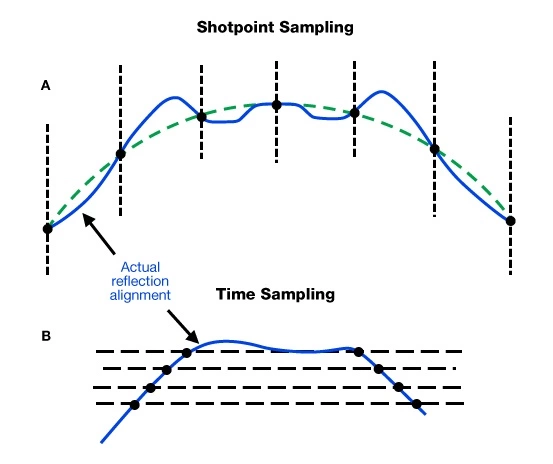
To be completely sure, therefore, it is necessary to time the reflection at least twice for each cycle of undulation of the reflection surface. It is also necessary to apply the process of reconstitution (restoring the structure) before interpolating between these times for contouring purposes.

The best practice when working at an interpretation workstation is to follow the sampling theorem, because then the interpretative software program can handle the resulting large volumes of data. In practice, however, interpreters disregard the sampling theorem when interpretation is done by hand because the volume of interpretation work would be too much. So, we bypass the sampling theorem by making some reasonable judgements, and by applying some reasonable standard processes:

• During picking, we ignore or smooth all small-scale trace-to-trace variations which we interpret to be due to noise, poor static corrections, or artefacts of the seismic method. In doing this, we are applying the criterion of geological plausibility.
• We look at the sections overall, in terms of the exploration play, and judge how much of the relief in the reflection surface is material; anything less than this we judge to be an artefact of the acquisition process and therefore of no importance to finding oil or gas.
• We select a contour interval which provides at least two contours (and preferably three or four) over this minimum significant relief.
• If we wish to time the picked reflection at a regular progression of times, we do this at the chosen contour interval. In this case, no interpolation of times is necessary in the contouring, and so we are not at risk for failing to reconstitute the data samples.
• If we wish to time the picked reflection at a regular progression of shotpoints, we look at the sections again, and decide what convenient shotpoint interval corresponds approximately to the contour interval on the steepest flanks of the smallest material relief. In this case we are at risk for failing to reconstitute. This can be seen in Figure 1A; if it happens that the times at A and B are 2.007 and 1.987 seconds respectively, then a simple interpolation of the 2.000 second contour is significantly in error. (As noted above, this problem does not arise if we time at the chosen contour interval.) When we elect to time on a regular progression of shotpoints, therefore, we err on the side of caution, and adopt shorter intervals if there is any doubt.
• Whether we sample regularly in time or in shotpoints, the major protection against our disregard of the sampling theorem is that we mark on the map the position and time of every significant high and every significant low, and the position and throw of every significant fault. This step saves us from mistakes like those in Figure 1. This should be a standard practice.
• Finally, we gain additional confidence and insurance by marking on the map zones of extended monoclinal dip and of zero dip.

Sensible modification of these rules may be indicated in practice, depending on the scale of the sections, the eye and hand of the interpreter, the software program available, the admissibility of skipping some measurements over featureless zones, and whether the timing is to be done by the interpreter or by a technician. As indicated by the examples in the text, the important thing is to learn by doing; a variety of examples quickly shows the dangers of violating the sampling theorem, and quickly provides practical reasons for the choice between regular intervals of time and regular intervals of shotpoints.