Rock Deformation

Time-Dependent Processes

It is beyond the scope of this introduction to geomechanics to fully address time-dependent rock deformation. However, it should be noted that fluid flow and rock creep are two processes that occur on time scales relevant to reservoir operations. These processes can be treated using sophisticated geomechanical models that are available commercially.

Fluid Flow

One of the most important time-dependent processes is the coupling between fluid flow and rock deformation. Recall that poroelasticity describes the coupling between rock and fluids. In a producing reservoir the fluid pressure is a function of time. Therefore, the effective stress and all processes that depends on effective stress changes with time. The aim of conventional reservoir modeling is to predict the time evolution of production and reservoir pressure over the life of a field. In the emerging field of reservoir geomechanics, modeling is focused on the coupling of fluid flow and reservoir deformation. Observable manifestations of reservoir deformation include reservoir compaction, grain crushing, and the concomitant reduction in permeability, massive solids production, fault activation, and 4D seismic effects.

Rock Creep

Rock creep is a time-dependent process leading to rock failure at shear stress levels that are significantly less than the short-term strength of the material. A characteristic strain-time curve for rock creep is shown in Figure 1.

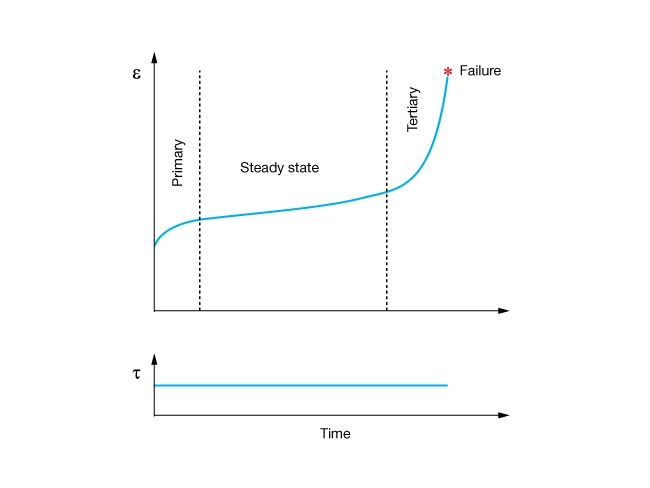
The creep mechanism operates at low temperatures and pressures encountered in hydrocarbon reservoirs. Creep is observed in strong brittle rocks such as granite as well as weak ductile material such as chalk (Rhett, 1990). Creep can reduce the long-term strength of rocks by as much as 50-70%. The time to failure ranges from minutes to years and is an increasing function of the applied shear stress (Farmer 1983). Figure 1 shows a schematic of a creep curve. The curve is divided into three phases:

• Primary, or transient, creep is characterized by the initial loading of the rock which deforms elastically and is followed by a decreasing strain rate.
• Secondary or steady state creep is characterized by an extended period of time where the strain rate gradually increases.
• Tertiary creep is a relatively short period where strain rate accelerates until the rock fails.

Pressure Solution

Pressure solution is a deformation mechanism associated with the mechanical compaction of rock. Pressure solution operates at the grain scale and involves the dissolution of material at high-stress grain-to-grain contacts. Stylolites are geologic structures produced by pressure solution Figure 2.

Bedding plane stylolites are commonly observed in carbonates and less frequently in sandstones. Tectonic stylolites form at high angles to bedding and are structurally aligned perpendicular to the direction of maximum compressive stress. Stylolites constitute a plane of weakness for tensile stress applied normal to the stylolite. They also are potential fault surfaces as the shear strength of the stylolite is less than the intact carbonate.

The stylolites in this figure are dark saw-tooth like structures oriented parallel with bedding. The dark material is the insoluble residue from the dissolved carbonate.

Crystal Plasticity

Deformation by crystal plastic processes generally occurs at great depth and over geologic time. Crystal plasticity involves thermally activated processes that operate at grain boundaries or propagate as dislocations within a crystal lattice. It is an important deformation mechanism in very low porosity mono-mineralic rocks where other mechanisms do not operate. At depth and temperature ranges of most reservoirs crystal plastic deformation mainly occurs in evaporates such as salt.

Salt deforms by dislocation creep and solution precipitation controlled grain boundary sliding (Zavada et al., 2009). Plastic deformation in salt impacts drillers who frequently encounter tight hole conditions when drilling through salt deposits.

Deformation Mechanisms and Mohr’s Stability Diagram

Knowledge about which deformation mechanisms can be mobilized in a given volume of rock is a requirement for completing a Mohr’s stability diagram. Understanding a rock’s microstructure and the existence or absence of weak planes helps to select appropriate failure criteria used to predict rock deformation and the state of stress.

Knowledge of the brittle-ductile transition pressure is important for reservoir optimization because it indicates whether production-induced pressure changes will cause the rock to deform in a brittle or ductile manner. A brittle response such as fracturing and faulting can lead to increased permeability as well as introduce a permeability anisotropy. A ductile response, such as compaction can lead to a reduction of porosity and permeability and possibly to massive solids production. Compaction in the reservoir can lead to faulting, causing collapse in the overburden. Elastic response to reservoir pressure change will change the in-situ stress and elastic wave velocities that may only be observable in time-lapsed seismic (4D) survey data.

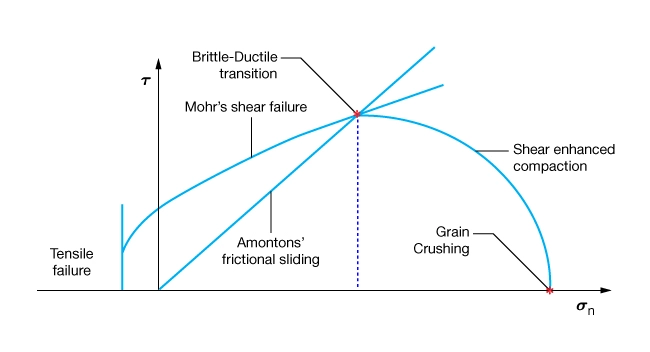
The Mohr’s stability diagram shown in Figure 3 illustrates the relationship between the four deformation mechanisms and the state of stress.

To simplify the description of the plot, we will ignore the rock’s non-linear behavior beyond the yield stress (segment 3 in Figure 4).

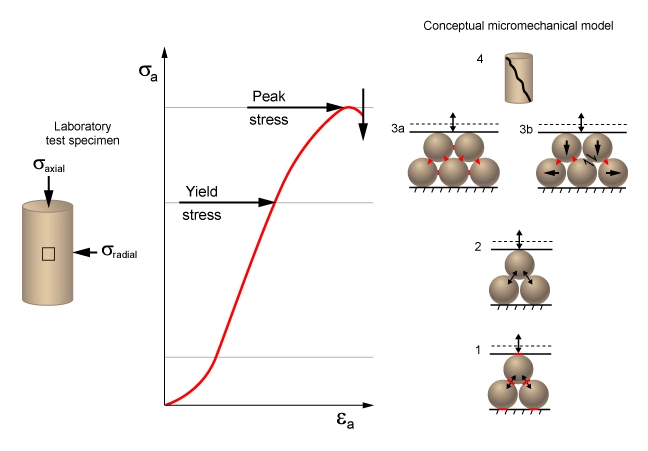
It is assumed that the rock deforms elastically until it satisfies one of the failure criteria. Remember also that no scale is implied by the diagram. The diagram could equally apply to a cubic millimeter of rock on a wellbore surface or to a cubic kilometer rock representing an oilfield.

Referring to Figure 3, elastic deformation is the dominant process for states of stress that do not intersect any of the failure criteria.

If a failure criterion is met at normal stresses less than the brittle-ductile transition pressure, the rock deforms in a brittle manner and fractures.

If a rock contains pre-existing planes of weakness, the rock deforms elastically until the state of stress satisfies the frictional sliding criterion on critically oriented surfaces. In the absence of weak planes, the rock deforms elastically until the state of stress intersects the tensile or shear fracture criterion.

If a failure criterion is met at normal stresses greater than the brittle-ductile transition pressure, the rock deforms in a ductile manner and flows. In situations where the shear stresses are very low, the rock behaves elastically until the effective normal stress reaches the grain-crushing criterion.