Horizontal Drilling | What is a horizontal drilling?

22 minutes read

Horizontal Drilling, Horizontal Wells, Horizontal Well, Directional and Horizontal Drilling

Horizontal Targeting

During drilling toward a horizontal target with a constant build rate, if the azimuth is found to be off the target, it is important to find an intermediate point at which the tool-face angle can be changed from right to left (or from left to right) to negate some of the change in azimuth while continuing the desired constant build rate (Schuh, 1989). The situation is shown in Figure 1.

Guo et al. (1993) presented a method to accurately determine this intermediate point and other related parameter values. The relevant equations are illustrated in Figure 2 (Guo et. al’s method for horizontal targeting).

Method for horizontal targeting, Build tangent section, Trajectory Planning, Horizontal Wells, Horizontal Well, Directional and Horizontal Drilling — **FIGURE 2**

The inclination angle at the intermediate point is expressed as

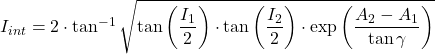$I_{int} = 2 \cdot \tan^{-1}\sqrt{\tan \left ( \dfrac{I_{1}}{2}\right ) \cdot \tan \left ( \dfrac{I_{2}}{2}\right ) \cdot \exp \left ( \dfrac{A_{2}-A_{1}}{\tan \gamma } \right )}$ (1)

The change in azimuth from point 1 to the intermediate point is

$A_{1-int}= \tan \gamma \cdot \ln \left [ \dfrac{\tan \left (\dfrac{I_{int}}{2} \right )}{\tan \left ( \dfrac{I_{1}}{2} \right )} \right ]$ (2)

The length to drill from point 1 to the intermediate point is

$\Delta L_{1-int}= \dfrac{\left ( I_{int} -I_{1}\right )}{B}$ (3)

The tool face angle to set is

$\gamma = \cos ^{-1}\left ( \dfrac{B}{D} \right )$ (4)

where B is the designed build rate and D is the deflection capacity of the tool. After the intermediate point is reached, the tool face should be re-oriented to the opposite direction in order to hit target at point 2. The tool face angle to set is

$\gamma = -\cos ^{-1}\left ( \dfrac{B}{D} \right )$ (5)

The change in azimuth from the intermediate point to point 2 is

$\Delta A_{int-2}= \tan \left ( -\gamma \right ) \cdot \ln \left [ \dfrac{\tan \left ( \dfrac{I_{2}}{2} \right )}{\tan \left ( \dfrac{I_{int}}{2} \right )} \right ]$ (6)