Fundamental Concepts of Reservoir Geomechanics

23 minutes read

Anisotropy

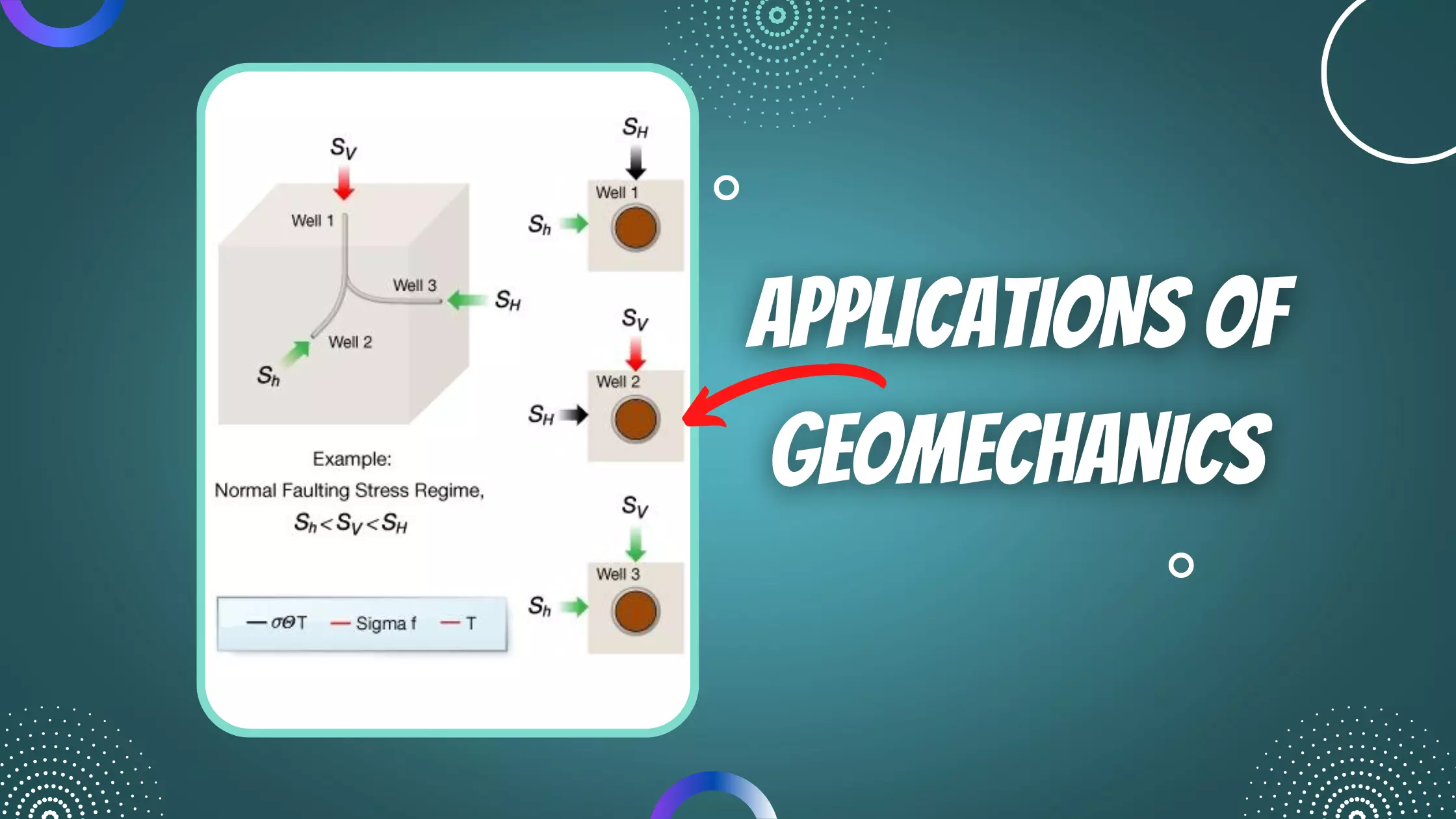
Anisotropic materials are characterized by physical and transport properties that vary with direction in the material. These include elastic moduli, elastic wave velocity, permeability, and thermal parameters among others. Rock anisotropy impacts reservoir development and completion decisions in fractured reservoirs, tight gas sand reservoirs, and shale gas reservoirs. For example, where should producer-injector well pairs be located, which intervals should be perforated, and how much fluid should be pumped for each hydraulic fracture?

Intrinsic Anisotropy

Intrinsic anisotropy is caused by alignment of minerals, sedimentary layering, or natural fractures. Figure 1 illustrates how homogeneous distributions of intrinsic rock properties can lower a rock’s elastic symmetry. For each diagram, the number of independent elastic constants required to characterize the material is indicated. The higher the number, the lower the symmetry, and the more difficult it is to quantify the elastic moduli.

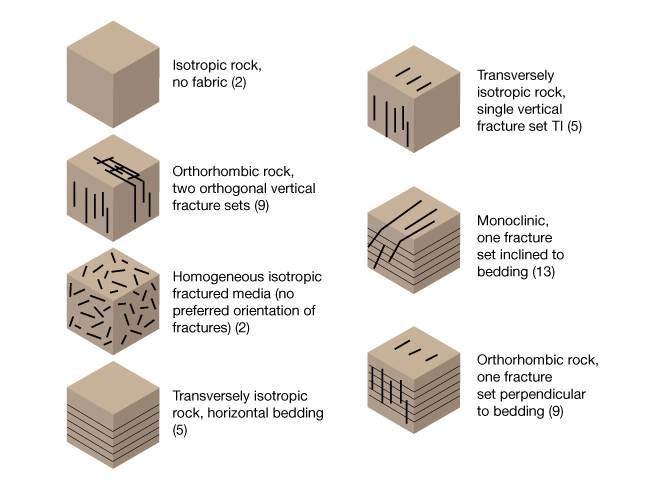
Elastic Symmetry of Rock

Finely laminated sedimentary rock such as shales and mudstones often possess transverse isotropy (TI) with respect to elastic moduli and rock strength. The properties of TI media are independent of direction in the plane of layering but they are different than properties in planes perpendicular to the layering. For example, the Young’s modulus and compressive strength for shale is often greater when measured in the plane of bedding than when measured perpendicular to layering. If the layering of a TI material is horizontal, it may be referred to as a TI-V material where the V indicates a vertical axis of rotational symmetry. TI materials are characterized by five independent elastic moduli. Many shale gas reservoirs are transversely isotropic. A deck of playing cards is a useful analog for TI-V shales.

TI and TI-V, Fundamental Concepts of Reservoir Geomechanics, Geomechanics — **Figure 2**: TI and TI-V

Fractures in an otherwise isotropic material can also impart anisotropy. For example, a TI-V shale would become an orthorhombic material if it contains fractures oriented perpendicular to bedding. A single set of parallel vertical fractures may create a transverse isotropy with the axis of rotational symmetry in the horizontal plane. This medium is called TI-H.

TI-H, Fundamental Concepts of Reservoir Geomechanics, Geomechanics — **Figure 3**: TI-H

If the medium contains two sets of fractures, oriented 90 degrees to one another, the material may possess orthorhombic elastic symmetry. Orthorhombic materials are characterized by nine independent material parameters. TI-V shale could also possess orthorhombic symmetry if it contains a single set of vertical fractures.

Orthorhombic with orthogonal fractures, Fundamental Concepts of Reservoir Geomechanics, Geomechanics — **Figure 4**: Orthorhombic with orthogonal fractures

As soon as the layering and fractures are not orthogonal, the elastic symmetry is reduced dramatically, and direct measurement of the elastic properties becomes intractable in the field using current seismic or well logging measurements. Laboratory measurements are the only practical way to obtain elastic moduli of materials with symmetry lower than TI.

Orthorhombic with perpendicular fractures, Fundamental Concepts of Reservoir Geomechanics, Geomechanics — **Figure 5**: Orthorhombic with perpendicular fractures

However, if a material contains a homogeneous distribution of randomly oriented fractures it behaves as a homogeneous isotropic medium in an un-stressed state (Sayers and Kachanov, 1995).

Homogenous, Fundamental Concepts of Reservoir Geomechanics, Geomechanics — **Figure 6**: Homogenous

Stress-Induced Anisotropy

A homogeneous isotropic material may become anisotropic under the influence of externally applied stress. Stress induced anisotropy is best developed in materials containing compliant grain contacts, micro cracks or fractures. The key is the existence of compliant elements. If all three principal stresses are non-zero, and the compliant elements are isotropically oriented, the rock acquires an orthorhombic elastic symmetry. If the compliant elements are not isotropically oriented, then the symmetry of the stress-induced anisotropy will be no higher than that of the compliant rock fabric. In the special case where the axes of principal stress are aligned with the compliant fabric, the symmetry of the stress-induced anisotropy and the fabric will be the same. This alignment occurs when the micro cracks and fractures are a direct result of the applied stress.

Elasticity of Transversely Isotropic Materials

In-situ stress profiles through anisotropic shale-gas reservoirs can differ substantially compared with isotropic reservoirs. Therefore it is important for hydraulic fracturing operations to take account of elastic anisotropy (Thiercelin and Plumb, 1991). In principal coordinates, the stress-strain relations for a TI-V elastic solid are (Amedai et al., 1987):

$\varepsilon _{xx} = \dfrac{\sigma _{xx}}{E} - \dfrac{\nu}{E}\sigma _{yy} - \dfrac{\nu'}{E'}\sigma _{zz}$

$\varepsilon _{yy} = - \dfrac{\nu}{E}\sigma _{xx} + \dfrac{\sigma _{yy}}{E} - \dfrac{\nu'}{E'}\sigma _{zz}$

$\varepsilon _{zz} = - \dfrac{\nu'}{E'}\sigma _{xx} - \dfrac{\nu'}{E'}\sigma _{yy} + \dfrac{\sigma _{zz}}{E'}$

where $E_x$ , $E_y$ , $E_z$ are the Young’s moduli in the $x$ , $y$ , $z$ directions respectively, $\nu_{x y}$ , $\nu_{y x}$ , $\nu_{z x}$ are Poisson’s ratios such that the Poisson’s ratio $\nu_{ij}$ characterizes the strain response in the $j$ direction due to a uniaxial stress applied in the $i$ direction. Furthermore:

$E_x = E_y = E$

$E_z = E'$

$\nu_{xy} =\nu_{yx} \equiv \nu$ , and

$\nu_{zx} =\nu_{zy} \equiv \nu'$

Anisotropy complicates analysis and modeling of some fractured shale reservoirs. As a consequence, rock anisotropy is frequently ignored—this is not recommended. Given today’s commercial logging software technology, TI-V is the lowest elastic symmetry that is normally included in geomechanics applications.