Fundamental Concepts of Reservoir Geomechanics

23 minutes read

Mohr’s Circle

Contents

Mohr’s Circle Mohr’s Circle Representations Stress Concentrations

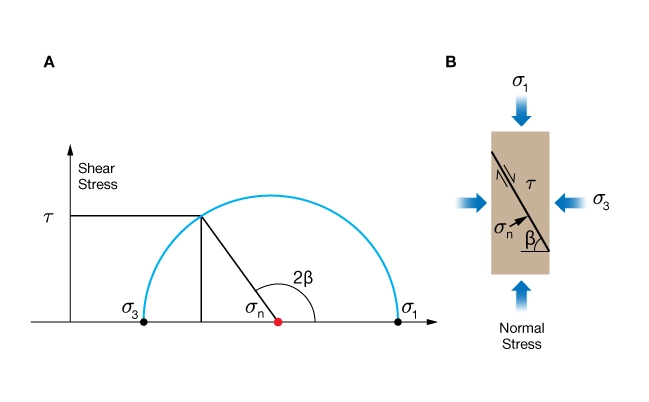
Mohr’s circle is a concise graphical representation of the state of stress in a solid body. It is named after the 19^th century German engineer Christian Otto Mohr. This diagram is frequently used to summarize the state of stress in a sedimentary basin or at a point on the surface of a wellbore.

Normal stresses are plotted on the abscissa; shear stresses are plotted on the ordinate. It is common practice in geomechanics to know the principal stresses rather than the shear and normal stresses on a particular plane. Given principal stresses, Mohr’s circle may be used to calculate the shear and normal stresses acting on any plane whose normal vector is inclined $\beta s$ degrees to the direction of $\sigma _1$ (Figure 1).

Mohr's circle, Fundamental Concepts of Reservoir Geomechanics, Geomechanics — **Figure 1**: Mohr’s circle

Given any two principal stresses, such as $\sigma _1$ and $\sigma _3$ , $t$ the center of Mohr’s circle plots on the abscissa at:

$\sigma _n = \dfrac{1}{2} \left( \sigma _1 + \sigma _3 \right)$

The maximum shear stress is given by the radius of the circle $R$ :

$R = \dfrac{1}{2} \left( \sigma _1 - \sigma _3 \right)$

Mohr’s Circle Representations

A Mohr’s circle representation of the state of stress in 3 dimensions is illustrated in Figure 2. It can be seen that the greatest shear stress in the rock mass is determined by the difference between the maximum, $\sigma _1$ , and the minimum, $\sigma _3$ , principal stresses.

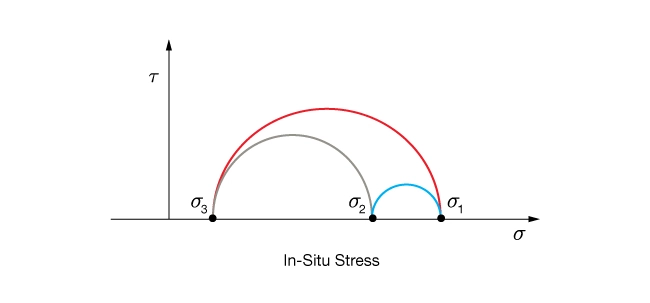
Mohr's circle in 3 dimensions, Fundamental Concepts of Reservoir Geomechanics, Geomechanics — **Figure 2**: Mohr’s circle in 3 dimensions

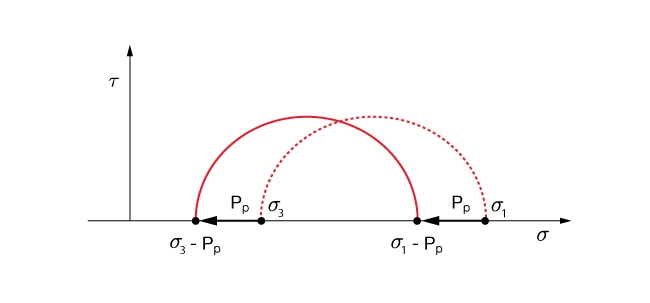
Figure 3 shows the Mohr’s circle representation of Terzaghi’s effective stress concept. Notice that the introduction of pore fluid pressure shifts the state of stress to the left, thus reducing the normal stress on planes in the rock mass. Note also that shear stress is unchanged.

Mohr's circle utilizing Terzaghi's effective stress concept, Fundamental Concepts of Reservoir Geomechanics, Geomechanics — **Figure 3**: Mohr’s circle utilizing Terzaghi’s effective stress concept

Stress Concentrations

Analysis of stress concentrations has great utility in geomechanics. Griffith (1921) used stress concentrations to explain the anomalously low strength of real materials compared to the theoretical strength of atomic bonds. Brace (1961) used Griffith’s theory to explain the strength of granular rock as a function of grain-size. However, one of the most useful solutions for geomechanics was developed by another 19^th century German engineer Ernst Gustav Kirsch. Kirsch developed equations that describe the elastic stress concentrations around a circular hole in an infinite plane subjected to a tensile stress in one direction (Kirsch 1898). The Kirsch equations form the basis for predicting the initiation of hydraulic fractures, wellbore instability and sand production. They also are the basis for earth stress analysis using borehole images.

$\sigma _{rr} = \dfrac{\sigma}{2} \left( 1 - \dfrac{a^2}{r^2} \right) + \dfrac{\sigma}{2} \left( 1 + 3\dfrac{a^4}{r^4} - 4\dfrac{a^2}{r^2} \right) \cos 2\theta$

$\sigma _{\theta \theta} = \dfrac{\sigma}{2} \left( 1 + \dfrac{a^2}{r^2} \right) - \dfrac{\sigma}{2} \left( 1 + 3\dfrac{a^4}{r^4} \right) \cos 2\theta$

$\tau _{r\theta} = \dfrac{\sigma}{2} \left( 1 - 3\dfrac{a^4}{r^4} + 2\dfrac{a^2}{r^2} \right) \sin 2\theta$

Kirsch’s solution shows that the introduction of a hole into a stressed plane creates stress concentrations at two orthogonal positions around the circumference of the hole (Figure 4).

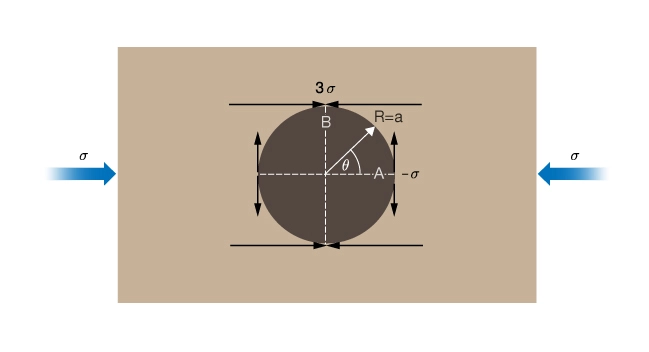
Stress related to a borehole, Fundamental Concepts of Reservoir Geomechanics, Geomechanics — **Figure 4**: Stress related to a borehole

One position is located along the direction of the maximum applied stress (A) at $\theta =$ 0 and 180 degrees. The other position is located at (B) $\theta =$ 90 and 270 degrees to the applied stress. The stress concentration is greatest at the surface of the hole $(r = a)$ and decays with increasing applied compressive stress $(\sigma)$ . At B, the stress concentration is compressive and equal to $3\sigma$ . It is the orientation of the stress concentration with respect to externally applied stress that is of great utility to in-situ stress analysis.