Shale Content | Shale Content and Petrophysical Evaluation

28 minutes read

Cation Exchange Capacity Model

An understanding of the nature and distribution of the shale elements within shaly sandstone sequences (Figure 1) in conventional resource reservoirs is critical for their correct reservoir characterization, particularly for low resistivity, low contrast and laminated shaly sandstones (Figure 2). Various techniques have been developed to address the petrophysical interpretation of shaly sandstone reservoirs, one of which uses a cation exchange capacity model (Figure 3).

Shaly sandstone sequence, shale content, Shale composition, Petrophysical analysis, Shale reservoir characterization, Porosity evaluation, Shale mineralogy, Petrophysical properties, Organic matter content, Shale gas potential, Petrophysical modeling, Clay content analysis, Shale permeability, Petrophysical interpretation, Shale formation evaluation, Total organic carbon (TOC), Shale geomechanics, Petrophysical parameters, Brittle shale, Shale facies analysis, Petrophysical logs, Shale porosity types, Petrophysical measurements, Shale core analysis, Effective porosity, Shale pore structure, Petrophysical evaluation methods, Shale water saturation — **Figure 1**: Shaly sandstone sequence

Finely laminated shaly sandstone formation outcrop, shale content, Shale composition, Petrophysical analysis, Shale reservoir characterization, Porosity evaluation, Shale mineralogy, Petrophysical properties, Organic matter content, Shale gas potential, Petrophysical modeling, Clay content analysis, Shale permeability, Petrophysical interpretation, Shale formation evaluation, Total organic carbon (TOC), Shale geomechanics, Petrophysical parameters, Brittle shale, Shale facies analysis, Petrophysical logs, Shale porosity types, Petrophysical measurements, Shale core analysis, Effective porosity, Shale pore structure, Petrophysical evaluation methods, Shale water saturation — **Figure 2**: Laminated shaly sandstone sequence displayed as a slabbed full diameter core

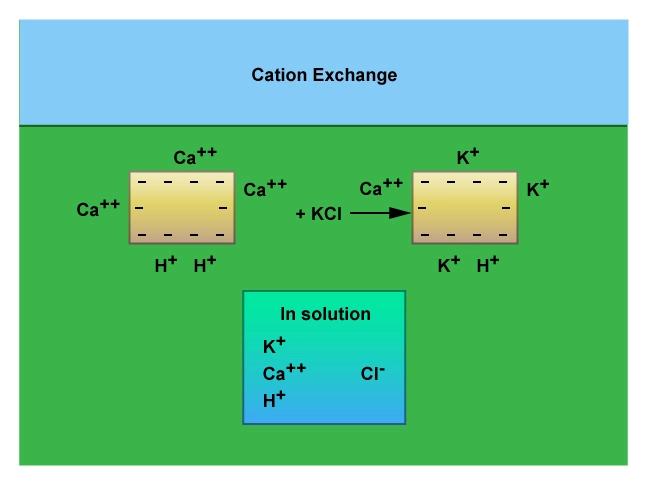
Cation exchange illustration, shale content, Shale composition, Petrophysical analysis, Shale reservoir characterization, Porosity evaluation, Shale mineralogy, Petrophysical properties, Organic matter content, Shale gas potential, Petrophysical modeling, Clay content analysis, Shale permeability, Petrophysical interpretation, Shale formation evaluation, Total organic carbon (TOC), Shale geomechanics, Petrophysical parameters, Brittle shale, Shale facies analysis, Petrophysical logs, Shale porosity types, Petrophysical measurements, Shale core analysis, Effective porosity, Shale pore structure, Petrophysical evaluation methods, Shale water saturation — **Figure 3**: Cation exchange illustration

Physical chemists can measure the ability of a rock, mineral or crystal surface to absorb water by finding the number of sites available for ionic exchanges (Figure 4). This is termed the cation exchange capacity (CEC). Different formation rock types and their constituent minerals have different CEC values. Quartz, which is the primary component of all sandstones, has a very low cation exchange capacity (Figure 5). Illite, smectite and montmorillonite clays, as a consequence of their high surface areas, have much higher CEC values.

Building blocks of clays (left), and cation exchange schematic for some common clays (right), clay content, Shale composition, Petrophysical analysis, Shale reservoir characterization, Porosity evaluation, Shale mineralogy, Petrophysical properties, Organic matter content, Shale gas potential, Petrophysical modeling, Clay content analysis, Shale permeability, Petrophysical interpretation, Shale formation evaluation, Total organic carbon (TOC), Shale geomechanics, Petrophysical parameters, Brittle shale, Shale facies analysis, Petrophysical logs, Shale porosity types, Petrophysical measurements, Shale core analysis, Effective porosity, Shale pore structure, Petrophysical evaluation methods, Shale water saturation — **Figure 4**: Building blocks of clays (left), and cation exchange schematic for some common clays (right)

Waxman and Smits (1968) derived an equation to express the water saturation, S_w, in shaly sandstones as a function of the cation exchange capacity of the clay disseminated in the sandstone formation, as follows:

$\dfrac{1}{R_t} = \dfrac{S_w^2}{F^* \cdot R_w} + \dfrac{B\cdot Q_v \cdot S_w}{F^*}$

Where:

F^∗ and Sw refer to the formation factor and water saturation, respectively, of the total interconnected pore space.

B is a constant that is dependent on the value of the formation water resistivity, R_w.

Q_v is the cation exchange capacity (CEC) per unit pore volume, normally established by the following equation:

$Q_v = \dfrac{CEC\cdot (1 - \phi )\cdot \rho _{ma}}{100\cdot \phi }$

This method, although based on sound laboratory measurements and good petrophysical principles, lacks a critical factor to enable its universal application: the direct availability of CEC values from either LWD or wireline well log measurements. Correlations for a given field can be made between full diameter core measurements of CEC and other well log measurements.

Modifications of the Waxman-Smits method by Waxman and Thomas (1974) and then by Juhasz (1981) have made it more directly applicable to measurements from well logs. Juhasz defined the cation exchange capacity per unit pore volume, Q_v, in terms of the effective and total porosity as it applies to the dispersed shale fraction of the sand, as proposed in the original Waxman-Smits technique. Juhasz then demonstrated that Q_v, as a function of the bound water saturation, is dependent on the shale distribution. Laminated shale is a bulk volume conductor. Exchangeable cations from the shale laminae are not available to the laminar sand fraction effective pore space and should not be included in the determination of Q_v, or dispersed shale-bound water conductivity in the sand.

A comparison of the Waxman-Smits and the Juhasz normalized Q_v (Q_vn) dual water models, after removal of the laminar shale effects, demonstrates that these models are equivalent if the correct conductivity of the bound water for the dispersed shale component can be determined directly.

Unfortunately, no simple, practical and readily available means exists to use the cation exchange capacity interpretation petrophysical technique if only well log data are available. Mollison et al. (2000) discussed using a tensor petrophysical model approach to reconcile the normalized Q_v models. The tensor petrophysical model determines the laminar shale volume and laminar sandstone conductivity from vertical and horizontal conductivities derived from electrical anisotropy. The volume of dispersed shale and the total and effective porosities of the laminar sandstone fraction are determined using a Juhasz volumetric approach. Removal of laminar shale conductivity and porosity effects reduces the shaly sandstone problem to a single dispersed shaly sandstone model to which the Waxman-Smits or equivalent equations can be applied.