Factors Affecting Measured Permeability Values
Air permeabilities measured in routine core analysis on rock samples from non-fractured reservoirs will give higher values than the actual in-situ reservoir permeability. The degree of difference is dependent upon the magnitude of the permeability, as well as the pore geometry. The higher laboratory readings are caused by a combination of gas slippage (the Klinkenberg gas slippage effect), relative permeability, reactive fluids and overburden pressure effects.
The Klinkenberg Gas Slippage Effect
The flow of gas through porous media was investigated by Klinkenberg, who found that the permeability of a core sample was not constant, but varied as a function of the gas used to make the measurement as well as with the mean pressure existing in the core at the time of measurement. His investigations indicated that at low mean pressures, such as atmospheric pressure, the gas molecules are so far apart that they slip through the pore spaces with little friction loss, and generate a higher value of permeability. At higher mean pressures, 1000 psi (6895 kPa) or greater, the gas molecules are closer together and experience a friction drag at the side of the pore walls. This increases as higher mean pressure increases, with the gas acting more and more like a liquid. This means that the measured permeability value decreases as the reservoir, or laboratory, mean pressure increases.
Experiments show that a plot of the gas permeability versus the reciprocal mean pressure existing at the time of the gas permeability measurement forms a straight line that can be extrapolated to infinite mean pressure. This extrapolated value of permeability, referred to as the Klinkenberg permeability or equivalent liquid permeability, is lower than the measured gas permeabilities and is comparable to the permeability that would be obtained if the core were saturated with a non-reactive liquid such as oil. Figure 1 shows an example of this relationship for low permeability sandstone.
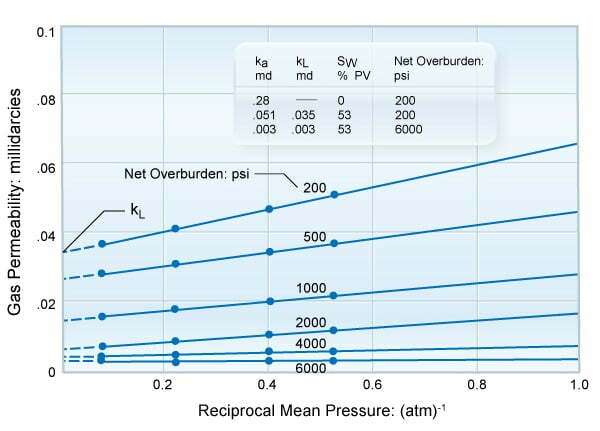
Steady state permeability measurements were made at each of the four points shown at each given net overburden pressure. The Klinkenberg value (kL) can be correlated with the value of permeability determined with air at the mean pressure normally used in the laboratory measurements. Table 1 shows examples of the relationship between the air permeability and Klinkenberg-corrected values for some sandstones. The correction, on a percentage basis, is greater in low permeability sands and becomes progressively smaller as the permeability value increases. The table represents the results of laboratory measurements on a suite of sandstone core samples that covered a wide range of air permeabilities.
| Non-corrected permeability (mD) | Klinkenberg corrected permeability* (mD) |
|---|---|
| 1.0 | 0.7 |
| 10.0 | 7.8 |
| 100.0 | 88.0 |
| 1000.0 | 950.0 |
Table 1: A Comparison of Uncorrected and Klinkenberg-corrected Air Permeability for Some Sandstones
In many historical core analysis reports, the measured air permeability was corrected to the Klinkenberg permeability value using correlations derived from such data as that shown in Table 1. These corrections have been found to be good approximations for many sandstones and some intergranular Iimestones. The correction is usually applied to plug-sized samples, and should not be applied to full diameter permeability measurements because the heterogeneity of most full diameter cores renders the correlations unreliable. If the need exists, Klinkenberg permeability values should be determined on each individual core plug sample.
The unsteady state permeameter allows the calculation of Klinkenberg permeability values on plug-sized samples and provides a second factor related to the pore geometry, expressed as b. The following equation relates air permeability to Klinkenberg permeability; knowledge of the Klinkenberg value and the “b” factor from the unsteady state tests allows calculation of the air permeability at any mean pressure desired.
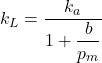
Because reservoirs exist at relatively high mean pressures, the Klinkenberg-corrected air permeability (equivalent liquid permeability) value is more representative of the reservoir value than the laboratory-measured ka value.
Impact of Reactive Fluids on Permeability
When a second fluid phase is present in a reservoir, the permeability to each phase is referred to as the effective permeability. The relative permeability to oil (Kro), gas (Krg) or water (Krw) is the ratio of the effective permeability of oil, gas, or water to the absolute permeability. In an oil or gas reservoir, the second phase present in the pore space is the interstitial water. The effective permeability to the hydrocarbon phase in a reservoir with interstitial water present will be less than the measured permeability to air after correction for Klinkenberg effects (absolute permeability). In high permeability rock with relatively low values of interstitial water, the presence of water reduces the gas or oil effective permeability only a minor amount below the absolute permeability. As the permeability of the rock decreases (a condition that is normally associated with a reduction in grain and pore sizes), the presence of water has an increasingly important and detrimental effect on the effective permeability to oil or gas.
Clays line the pore spaces of many formations and sometimes react with the coring, drilling or other fluids injected into the reservoir. This reaction commonly results in a reduction in permeability that can vary from minor to catastrophic. Two types of damage mechanism can result. One is a dispersal of clay particles and/or a physical tearing loose of clay platelets that subsequently block the pore throats and reduce the permeability. A second type of reaction involves clay swelling, which causes an increase in clay volume and the subsequent reduction in the cross-sectional area open to flow within the pore throats. Because of the difference in the mechanisms, each demands a different treatment for correction, but the effect of both is to cause the in-situ reservoir permeability to be lower than that measured in the laboratory.
Overburden Pressure Effects
Core samples, when first tested for routine core analysis measurements, usually have no net overburden pressures applied to them. When simulating reservoir conditions in the laboratory, it has been found that the application of overburden pressure reduces the permeability. Reduction in permeability of as little as 7% to as much as 100% has been reported for overburden pressures up to 5000 psi (34,475 kPa).
Table 2 shows some permeability reduction data for samples that ranged from well-cemented to unconsolidated. As has been noted in porosity measurements, the unconsolidated materials show the greatest percentage of permeability reduction with increasing overburden pressure. Generally, the percentage of permeability reduction with the application of net overburden pressure is greater than the reduction seen in porosity.
| Table 2: Permeability Reduction with Increasing Overburden Pressure | |||
|---|---|---|---|
| Net Overburden Pressure | Permeability (% of original) | ||
| Sandstone (well indurated) | Sandstone (unconsolidated) | Chalk | |
| 200 psi | 100% | 100% | 100% |
| 1000 psi | 96% | 72% | 97% |
| 3000 psi | 91% | 44% | 93% |
| 5000 psi | 86% | 35% | 60% |
| 7000 psi | 82% | 30% | 30% |
Experiments with flow through capillary tubes indicate that the quantity of fluid flowing through a capillary varies with the fourth power of the tube’s radius. As the value of air permeability is directly proportional to flow rate, small reductions in the pore radii caused by the application of overburden pressure result in correspondingly large reductions in permeability.
In any given reservoir, the effects of gas slippage, reactive fluids and overburden pressure may be great or small, significantly depending on the pore geometry. Laboratory results indicate that these factors become more important as the absolute permeability of a rock decreases. In some low permeability gas reservoirs, a high interstitial water level causes a significant reduction in the effective permeability, with further reductions caused by an increase in net overburden pressure and the gas slippage effect.
In a controlled experiment, a sample with an initial air permeability of 0.28 millidarcies was taken. When a non-mobile, interstitial water saturation of 53% of the pore space was introduced, the original air permeability determined on the dry core was reduced to an effective permeability of 0.051 millidarcies. These measurements were made with a minimum net overburden pressure of 200 psi (1379 kPa), to prevent air bypassing the core and flowing down the sample’s sides.
The Klinkenberg permeability value, obtained from the extrapolation of four measured air permeabilities at different mean pressures, showed a further reduction in effective permeability to 0.035 millidarcies. An increase in overburden pressure from 200 to 6000 psi (1380 to 41,370 kPa) resulted in a final effective permeability of only 0.003 millidarcies. This is approximately a 100-fold decrease in permeability in total.
 Petro Shine The Place for Oil and Gas Professionals.
Petro Shine The Place for Oil and Gas Professionals.



