Petro Shine The Place for Oil and Gas Professionals.
Related Articles
Build Curve Design
There are four basic build curve designs used in bringing a well from vertical to horizontal:
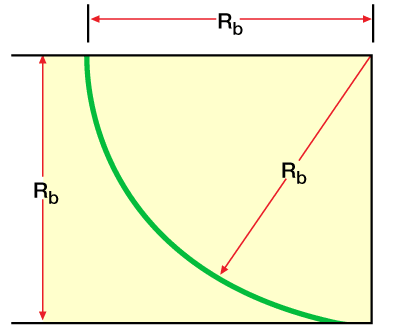
- single build (Figure 1)
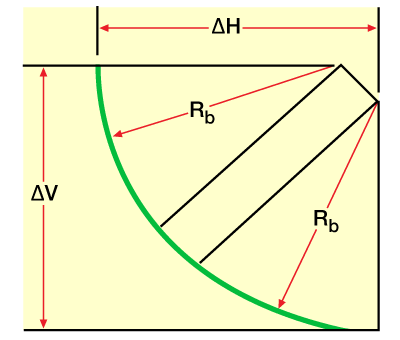
- simple tangent (Figure 2)
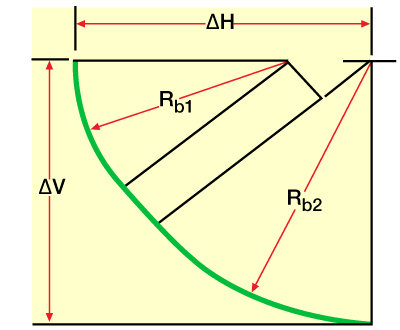
- Complex tangent (Figure 3)
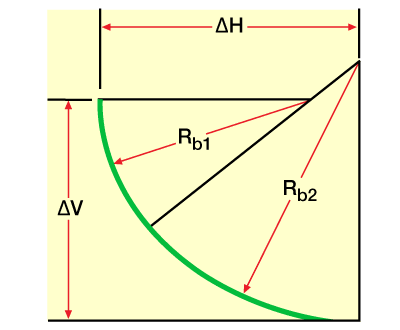
- Ideal (Figure 4)
The equations for designing these curve types are easy to derive, and are summarized below (Schuh, 1989).
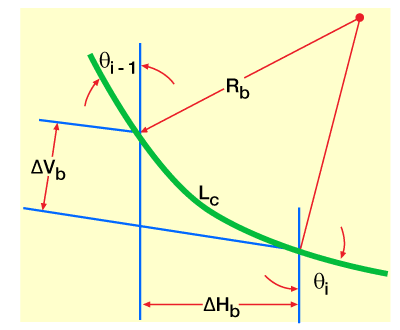
From Figure 5 (Circular arc),
(1)
(2)
(3)
where
Lc = length of curved section
Rb = build curve radius
BR = build rate angle
ΔHb = horizontal displacement of build curve section
ΔVb = vertical displacement of build curve section
θi, θi−1 = inclination angles at stations i and i−1, respectively, on build curve
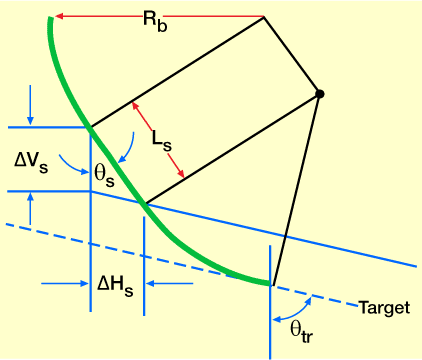
The straight section required to hit a sloping target (Figure 6) is
(4)
(5)
where
Ls = length of straight section
ΔHs = horizontal displacement of straight section.
ΔVs= height to target slope.
θs, θtr = straight section and target angles, respectively.
s = straight
tr = target
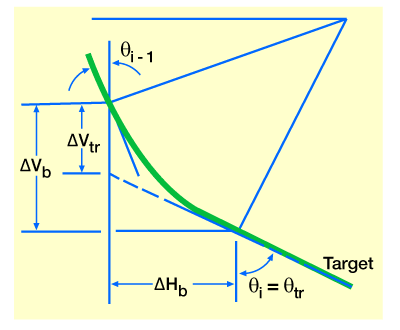
The build rate angle required to hit a sloping target (Figure 7) is
(6)
where
BR = build rate
Vtr = vertical height from target
(7)
(8)
(9)
The tool face angle required for the second build is
(10)
The dog-leg severity is
(11)
The azimuth change is
![\alpha = \left ( 57.3\cdot \tan \phi _{tf} \right )\cdot \ln \left [ \dfrac{\tan\left ( \dfrac{\phi _{1}}{2} \right ) }{\tan \left ( \dfrac{\phi_{i-1}}{2}\right )} \right ]](https://petroshine.com/wp-content/ql-cache/quicklatex.com-28fd7ab181c8d5334956c82b81c7df24_l3.png "Rendered by QuickLaTeX.com")
(12)
where
ϕtf = tool face angle, degrees
DL = dog-leg severity, degrees
BR1= first build rate angle
BR2 = second build rate angle
The required final curvature build rate, BRr, to hit a target is given by
(13)
where
θtr = target inclination angle
θi = present inclination angle
TVDtr = target true vertical depth
TVDi = target present true vertical depth
