Geodynamic models are mathematical and computational models used to study the processes that shape the Earth’s interior and its surface. These models simulate the movements of rocks and fluids, the distribution of heat, and the transfer of mass within the Earth’s interior, among other factors.
Geodynamic models are used to better understand a range of Earth processes, such as mantle convection, plate tectonics, volcanic eruptions, and seismic activity. They are also used to investigate the formation and evolution of the Earth’s crust and mantle, as well as the interaction between the Earth and its atmosphere and hydrosphere.
Introduction To Geodynamic Models
Geodynamic models are process/response models that estimate subsidence and heat flow histories of basins. We use these models to estimate values, like maturation levels or stratigraphic thicknesses, that we can compare to observed data. We can then use these models to predict subsidence and heat flow for portions of a basin and for time periods for which we have no data. We can also use models to predict the distribution of lithologies, stratigraphic architecture, source rock maturation, and migration histories relative to structural timing. By establishing how confident we are of these modeled outputs, we can assess the geologic credibility of subsequent interpretations or analyses.
Basin subsidence and heat flow are responses to tectonic processes that may induce heating events and that may add or remove loads above, within or beneath the lithosphere. Tectonic processes commonly involve both mechanical and thermal loads. We can estimate subsidence and heat flow histories by combining assumptions about load types, rheology structure, temperature structure, sediment fill histories, and lithospheric compensation and heat transfer mechanisms. Today, the most common geodynamic models include lithospheric stretching and cooling and supralithospheric loading models. However, when building a geodynamic model for a specific basin, we must determine the history of dominant tectonic processes (and thus loading and compensation mechanisms), the ranges in model parameters, and the initial and boundary conditions of the basin.
We use knowledge of the tectonic setting and history of a basin for two purposes in geodynamic modeling. First, we use this knowledge to determine the dominant tectonic processes that formed the basin, and to guide construction of a geodynamic model for that basin. What types of loads were important during basin formation? Did load type change during basin development? We commonly apply stretching and cooling models in extensional settings such as rifts, passive margins and transtensional basins, and use supralithospheric loading models in compressional settings, such as foreland and transpressional basins.
Second, by knowing the tectonic setting and history of a basin, we can estimate crustal composition, initial crustal and lithospheric thicknesses, temperature structure and lithospheric compensation mechanisms for the geodynamic model. For example, a basin formed on a tectonically stable continental crust may have initial crustal and lithospheric thicknesses of 30 km and 125 km, respectively. If the basin formed due to supralithospheric loading without an associated heating event, the lithosphere was probably rigid enough to compensate loads flexurally. In contrast, a basin formed by lithospheric extension on a previously cooled, failed rift might have an initial crustal thickness of only 10 km and the same lithospheric thickness of 125 km. The heating event caused by extension may thin and weaken the lithosphere sufficiently that an Airy compensation model is adequate for modeling load compensation.
We use stratigraphic, structural, tectonic, geochemical and geophysical data to infer model parameters, initial configurations and boundary conditions, and to evaluate the accuracy of a geodynamic model by comparing these data to model outputs. Geodynamic models must predict magnitudes and shapes of subsidence and heat flow that are consistent with data, such as time-temperature indicators and present heat flow and temperature structure, or with data analyses, such as geohistory and backstrip diagrams. The models must predict the evolution of accommodation space for sediment within a basin. This evolution is recorded in the stratigraphic architecture, and the volumes and distribution of facies within the basin. The models might also predict a present-day density structure from which we can model a gravity response and compare it to observed gravity measurements. The models must be consistent with known constraints on tectonic configurations and with evidence of tectonic activity, such as timing of the creation of oceanic crust or timing of fault movement within thrust systems. Using estimates of thermal conductivities of lithospheric material, the heat flow we predict using a geodynamic model must be consistent with igneous activity and metamorphic regimes.
We can not exactly reproduce or predict subsidence and heat flow within a basin using geodynamic models because models are simplifications and approximations of real-world process/response systems. We cannot reproduce the complexities of tectonics, sedimentation, compensation, heat transfer, or other processes within geodynamic models because of computer limitations, and/or an incomplete knowledge of the process/response systems. The data we use are always incomplete and uncertain. Our confidence in the subsidence and heat flow predictions of our model depends on the types of tectonic and sedimentation processes, compensation conditions and heat transfer mechanisms that we include in the model, the degree to which the model correctly approximates those processes, and the degree of uncertainty in the data we use to estimate initial configurations, boundary conditions and model parameters.
Kinematic Cooling Models Overview
Kinematic lithospheric cooling models simulate the basin subsidence and heat flow that arise from the conductive cooling and contraction of lithosphere following a heating event. Cooling models were originally applied to some sedimentary basins because the observed form of subsidence was similar to the form of subsidence of oceanic crust as it cools and subsides (Sleep, 1971). Because of this similarity, a similar mechanism – cooling and contraction – was assumed.
The two principal types of cooling models – plate and half-space – are based on different thermal boundary conditions. The cooling plate model predicts subsidence rates that decrease exponentially with age after cooling begins (Sleep, 1971; McKenzie, 1978). The cooling half-space model predicts subsidence proportional to the square root of age after cooling begins (Parsons and Sclater, 1977; Turcotte, 1980). Both models predict approximately the same subsidence histories for the first 70 My of cooling, but after 70 My the cooling plate model predicts subsidence that approaches an asymptotic value (Figure 1, Theoretical basin structure for cooling half-space and cooling plate models).
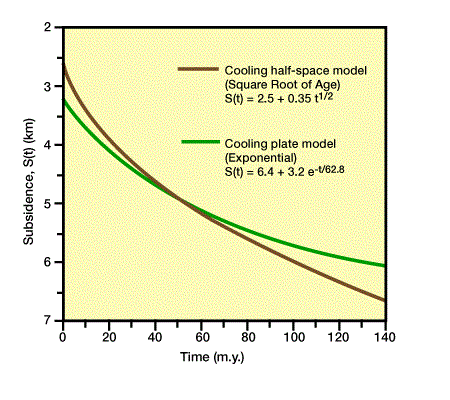
Observed subsidence histories for oceanic crust and some basins tend to more closely match a square root-of-age curve for the first 70 My and an exponential curve for ages greater than 70 My (Parsons and Sclater, 1977; Bond and Kominz, 1984).
Thermal doming due to active rifting is exactly balanced by subsidence during subsequent cooling. Therefore, there is no net subsidence or uplift, unless the dome is eroded before cooling, in which case, there will be a net subsidence.
Basin-scale accommodation space requires tectonic subsidence to depress the topographic surface below its initial elevation. Cooling models accomplish this by increasing the average density of the lithosphere (i.e., forming a new load) so that it becomes less buoyant and subsides below its initial elevation. Cooling models differ primarily in the tectonic processes that are assumed to heat the lithosphere and to create accommodation space. Such tectonic processes include metamorphism (Falvey and Middleton, 1981), dike intrusion (Royden, Sclater, and von Herzen, 1980), and crustal thinning by either lithospheric stretching (McKenzie, 1978) or erosion after thermally induced uplift (Sleep, 1971).
The most common cooling models are the lithospheric stretching model of McKenzie (1978) and its derivatives (e.g., Jarvis and McKenzie, 1980; Royden and Keen, 1980; Keen, Beaumont and Boutilier, 1981; Le Pichon and Sibuet, 1981; Watts and Steckler, 1981; Hellinger and Sclater 1983; Pitman and Andrews, 1985). Mechanically, these are the simplest models that can account for observed first-order effects of subsidence and heat flow within some basins. Lithospheric stretching is the mechanism for creating accommodation space that is most consistent with data used to estimate crustal thicknesses (e.g., seismic and gravity) and with stratigraphic reconstructions.
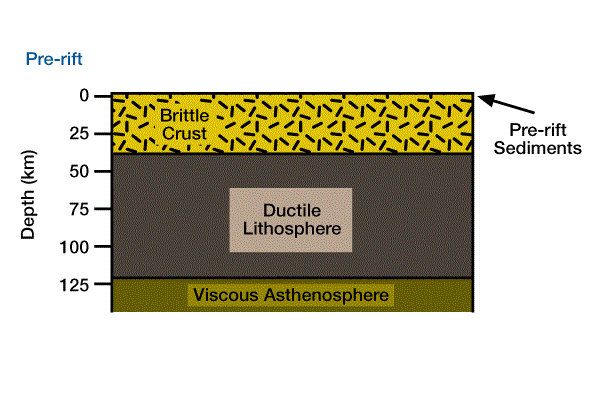
Stretching models estimate changes in surface elevation and heat flow histories due to lithospheric stretching caused by tectonic rifting (Figure 2, Stages of rifting of a continental to form a passive margin; Initial configuration.),
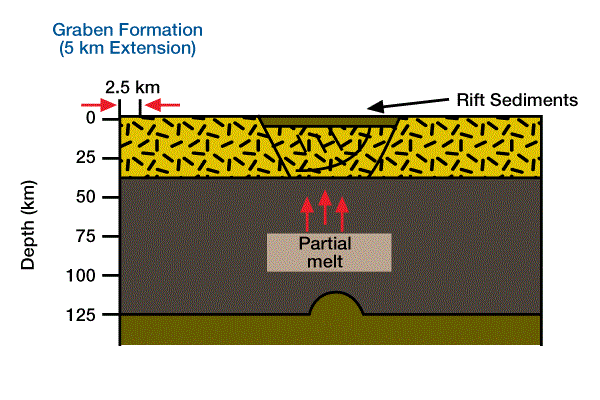
(Figure 3, With extension, a graben forms on brittle continental crust, and viscous asthenosphere rises, replacing ductile mantle lithosphere.),
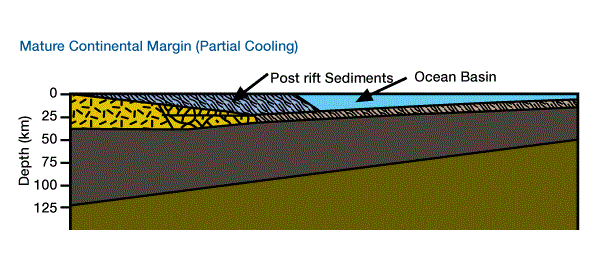
(Figure 4, A topographic bulge forms where mantle lithosphere is replaced with less dense viscous atmosphere; the flanks of the newly formed rift basin are eroded.

Brittle crust and ductile asthenosphere are stretched and thinned.), (Figure 5, Asthenospheric material reaches the surface of the earth, forming oceanic crust.

Stretching and thinning of continental crust ceases, and the continental moves away from the newly formed spreading ridge.), and (Figure 6, Accommodation space for post-rift sediments on a passive margin formed by cooling and contraction of mantle lithosphere.).
The brittle crust and ductile lithosphere extend and thin, and the newly created space is filled by rising hot, viscous asthenosphere. Stretching may be either a passive response to regional tension or an active response due to asthenospheric diapirism. Lithospheric stretching can progress through stages of graben formation, to a rift basin underlain by continental crust, to a rift basin attached to a spreading ridge, and ultimately to a mature passive margin.
The initial isostatic response to lithospheric extension and stretching can cause an immediate increase in average lithospheric density by thinning the mantle lid less than the crust. Stretching represents a balance between a tendency for uplift caused by increased buoyancy due to rising asthenosphere and a tendency for subsidence caused by decreased buoyancy due to increased average lithospheric density. The immediate response to stretching, before significant cooling occurs, is isostatic. With homogeneous stretching, subsidence occurs although the average lithospheric density does not change. According to Archimedes’ Principle, reducing the thickness of a floating object lowers the top of the object.
Uplift will cause erosion (e.g., on the flanks of the rift basin in Figure 4), and subsidence will create accommodation space for the accumulation of sediments (e.g., the center of the rift basin in Figure 3 and Figure 4). After extension ceases, the lithosphere gradually cools and contracts (increasing its average density), returns to its initial thickness, and subsides, creating accommodation space for additional sediments. The initial isostatic response can not be a function of density changes due to cooling.
Because rifting is associated with the formation of oceanic crust, which is one to two orders of magnitude less rigid than continental lithosphere, we assume that rigidities are low enough for Airy compensation to be an adequate model for this changing density structure. Consequently, we do not commonly consider flexural and temperature-dependent rigidities in these models.
 Petro Shine The Place for Oil and Gas Professionals.
Petro Shine The Place for Oil and Gas Professionals.



