Reservoir Fluid Flow and Natural Drive Mechanisms

54 minutes read

Solution Gas Drive and the Material Balance Equation

The material balance equation for a solution gas reservoir may be used for two purposes. If production data are available the MBE may be used to calculate the initial oil in place. When combined with Darcy’s law it may also be used to predict recovery versus pressure.

Quantifying Reservoir Performance, Calculation of Initial Oil In Place We will examine first the use of the MBE to calculate N, or initial oil in place. Once again, the MBE (ignoring rock and water compressibility) is

$N_{p}\, [B_{t}+(R{p} - R_{si})\, B_{g}] + W_{p}\, B_{w} = N\, (B_{t} - B_{ti})$

In order to simplify the paperwork, let us indicate the left hand side, which represents the total production in reservoir volumes, by the term F. We can also simplify the equation further, by substituting E_o for (B_t−B_ti), which represents the expansion of the oil and its associated gas. The MBE then becomes

$F = N\cdot E_{o}$

This is the equation of a straight line. A plot of F versus E_o should give a straight line passing through the origin with a slope equal to N (Figure 1). This solution method is known as the MBE as an equation of a straight line and is discussed in detail by Havlena and Odeh (1963, 1964).

Usually production data is tabulated on a monthly or quarterly basis. Average reservoir pressure for the same time periods is also tabulated. Using the PVT data available from a laboratory analysis or from correlations, F and E_o are calculated for the necessary time periods and plotted on rectangular coordinate paper. If there is no active aquifer the points should show a straight line trend. A straight line that results in the minimum standard deviation and that passes through the origin is drawn. The slope is N, the initial oil in place.

The mathematical requirement that the line should pass through the origin is very important. Whenever one deals with field data, there will be scatter of the data points. Without the above requirement it is conceivable that a straight line that minimizes the standard deviation without passing through the origin may be fitted to the plotted points. The MBE as an equation of a straight line dictates that the origin must be a point, and thus imposes a very important condition which must be satisfied for an acceptable solution.

Performance Prediction Techniques The MBE, together with the GOR equation derived from Darcy’s law (Equation 12), may be used to predict performance. Three methods are normally used, those developed by Tarner, Tracy, and Muskat (Craft and Hawkins 1959; Muskat 1949; Tracy 1955), as outlined below.

Tarner Method

In the Tarner method, one guesses at, or assumes, an incremental recovery of oil, ΔN_p resulting from an incremental decline in pressure. The incremental decline in pressure should not be taken as greater than 200 psia (1400 kpa). The incremental gas produced, ΔG_p due to ΔN_p is then calculated by two methods: the MBE, and the GOR equation. If the assumed ΔN_p is too large, ΔG_p calculated by the MBE will be too small, while that calculated by the GOR equation will be too large. Thus, the error in ΔNp results in two opposing errors in the ΔG_p values. The two ΔG_p values agree only when the assumed ΔN_p is correct. Specifically, the calculations proceed as follows:

1. Assume AN to be produced when the average reservoir pressure declines from p_j to p_j₊₁ (i.e., by Δp_j.

2. Use the MBE equation to calculate N_p R_p= G_p by

$G_{p_{j+1}} = \dfrac{1}{B_{g}} \left [ \left ( B_{t}-B_{ti} \right )-N_{p_{j+1}}B_{t} \right ]+N_{p_{j+1}}R_{si}$ ……….. (44)

Note in that, $N_{p_{j+1}}=$ sum of all the $\Delta N_{p_{j}}$ increments that have been produced. Thus

$N_{p_{j+1}}=\displaystyle \sum _{j=1}^{j+1}\Delta N_{p_{j}}$

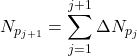
$G_{p_{j+1}}$ is the total gas produced. The calculations are made for one surface volume of oil, i.e., N=1.

3. Calculate the incremental gas produced $\Delta G_{p_{j}}$ due to $\Delta N_{p_{j}}$ by

$\Delta G_{p_{j}}=G_{p_{j+1}}-G_{p_{j}}$

where is the total gas produced corresponding to the average reservoir pressure $p_{j}$ and $G_{p_{j+1}}$ corresponds to the $p_{j+1}$ pressure.

4. Calculate S_o by

$S_{o_{j+1}}=\dfrac{\left ( 1-N_{p_{j+1}} \right )B_{o_{j+1}}\left ( 1-S_{wi} \right )}{B_{oi}}$

5. Calculate $S_{g}$ , if needed, $S_{g}=1-S_{o}-S_{wi}$

6. Determine $\tfrac{k_{rg}}{k_{ro}}$ corresponding to $S_{g}$ or $S_{o}$

7. Calculate R (i.e., GOR) by the GOR equation

$R_{j+1}=\left ( \dfrac{k_{rg}\mu _{o}B_{o}}{k_{ro}\mu _{g}B_{g}} \right )_{j+1} + R_{s_{j+1}}$

8. Calculate ΔG_p by

$\Delta G_{p_{j}}=\left ( \dfrac{R_{j+1} + R_{1}}{2} \right )\, \Delta N_{p_{j}}$

Compare $\Delta G_{p_{j}}$ calculated in Step 3 with that calculated in Step 8. If they agree within a reasonable tolerance, accept the assumed $\Delta N_{p_{j}}$ and continue the calculations by assuming a new $N_{p}$ corresponding to a new incremental pressure drop. The calculations are continued until an abandonment pressure is reached. If $\Delta G_{p_{j}}$ of Step 3 does not agree with that of Step 8, assume a new value for $\Delta N_{p_{j}}$ and repeat the calculations. Be guided by the observation that if $\Delta G_{p_{j}}$ of Step 3 is smaller than $\Delta G_{p_{j}}$ of Step 8, one needs to guess a smaller $\Delta N_{p_{j}}$ . value. The opposite is also true.

To illustrate the above method of calculation let us consider the following example. We want to calculate the incremental oil recovery by solution gas drive when the pressure declines from an original bubble-point pressure of 2500 psia to a pressure of 2300 psia.

Example 3

Given the following data:

p	B_o	R_s	B_g ⋅ 10³	μ_o	μ_g	B_t
$psia$	$\tfrac{RB}{STB}$	$\tfrac{Scf}{STB}$	$\tfrac{RB}{Scf}$	cp	cp	$\tfrac{RB}{STB}$
2500	1.498	721	1.048	.488	.0170	1.498
2300	1.463	669	1.155	.539	.0166	1.523

Also given:

$S_{g}$	$\tfrac{ k_{rg}}{K_{ro}}$
0	0
.06	0
.07	0.001
.09	0.009

$S_{wi} = 0.2$ , and $p_{b}=2500\ psia$

The solution is as follows:

1. Assume an incremental oil recovery $\Delta N_{p}=0.018$ to occur when the pressure declines to 2300 psia. Since the pressure at the beginning of the calculation step is the bubble-point value, then $\Delta N_{p}$ in this case represents the total recovery, i.e.,

$\sum \Delta N_{p}=N_{p}=0.018$

2. Solve for $\Delta G_{p}$ by MBE:

$\Delta G_{p} = \left [ \left ( B_{t}-B_{ti} \right )-N_{p}B_{t} \right ]\dfrac{1}{B_{g}}+N_{p}R_{si}$

$=\dfrac{1.523 - 1.498 - 0.018\cdot 1.523}{0.001155}+.018\cdot 721$

$=10.89\ scf \ \left ( 0.308\ m^{3} \right )$

$S_{o}=\dfrac{B_{o}}{B_{oi}}\left ( 1-S_{wi} \right )\left ( 1-N_{p} \right )=\dfrac{1.463}{1.498}\cdot 0.8\left ( 1-.018 \right )=0.767$

$S_{g}=1 - 0.2 - 0.767 = 0.033$

3. Calculate P by the GOP equation:

For $S_{g} = 0.033,\ \tfrac{k_{rg}}{k_{ro}} = 0$ , thus,

$R_{2300} = 0 + R_{s} = 669\left ( 119.41\ \tfrac{m^{3}}{m^{3}}\ at \ 17237.5\ KPa \right )$

$R_{2500} = 0 + R_{si} = 721\left ( 128.41\ \tfrac{m^{3}}{m^{3}} at \ 15858.5\ KPa \right )$

4. Calculate ΔG_p by the GOP equation:

$\Delta P_{g}=\left ( \dfrac{669 + 721}{2} \right )\cdot 0.018 = 12.51\ Mscf\ \left ( 0.3542\ m^{3} \right )$

$\Delta G_{p}$ calculated in Step 2 is not close enough to that of Step 4. Because the value of Step 2 is smaller than that of Step 4, our next guess will be to decrease $\Delta N_{p}$ . Let $\Delta N_{p} = 0.016$ . For this value $\Delta G_{p}$ by MBE will be 12.8 (.342 $m^{3}$ ), while that by the GOR will be 11.12 (0.3149 $m^{3}$ ). To arrive at the next guess one plots the assumed $\Delta N_{p}$ values versus the difference between the calculated $\Delta G_{p}$ values. The intersections of the line connecting the plotted points with the line of $A\left ( \Delta G_{p} = 0 \right )$ gives the next estimate of $\Delta N_{p}$ . In this example the intersection gives an estimate of $\Delta N_{p} = 0.01675$ .

For $\Delta N_{p} = 0.01675$ , $\Delta G_{p}$ by the MBE = 11.635 (0.3295 $m^{3}$ ), while that of the GOR equation = 11.640 (0.3296 $m^{3}$ ). This is a good check and the value is accepted.

The next step is to lower the pressure by another increment and to repeat the calculations. This is continued until an abandonment pressure is reached. The gives the oil recovery as a fraction.

Tracy Method

In Tracy’s method one guesses at R in place of $\Delta N_{p}$ The calculations proceed as follows:

1. Guess at a value of $R_{j+1}$ as the pressure declines from $p_{j}$ to $p_{j+1}$

2. Estimate the average R for the increment between $p_{j}$ and $p_{j+1}$ by

$R_{av}=\dfrac{R_{j}+R_{j+1}}{2}$

3. Calculate $\Delta N_{p_{j}}$ resulting from the drop in pressure to $p_{j+1}$ by

$\Delta N_{p_{j}}=\dfrac{B_{t+1}-B_{ti}+N_{p_{j}}\left ( R_{si}B_{g_{j+1}}-B_{t_{j+1}} \right )-G_{p_{j}}B_{g_{j+1}}}{B_{t_{j+1}}-\left ( R_{si}+R_{av} \right )B_{g_{j+1}}}$

where $N_{p_{j}}$ and $G_{p_{j}}$ are respectively the cumulative oil and gas produced at the average reservoir pressure $p_{j}$

4. Calculate $S_{o_{j+1}}$ by

$S_{o_{j+1}}=\dfrac{\left ( 1-N_{p_{j+1}} \right )\left ( B_{o_{j+1}} \right )\left ( 1-S_{wi} \right )}{B_{oi}}$

5. Determine $\tfrac{k_{rg}}{k_{ro}}$ = corresponding to $S_{o_{j+1}}$

6. Calculate R by

$R=\left ( \dfrac{k_{rg}}{k_{ro}} \right )\left ( \dfrac{\mu _{o}B_{o}}{\mu _{g}B_{g}} \right )_{j+1}+R_{s_{j+1}}$

Compare R of Step 6 with R of Step 1. If the comparison is favorable, accept and proceed to the next calculation increment; otherwise repeat the calculations starting with Step 1.

The advantage of Tracy’s method is that the calculation converges faster than in Tamer’s. This is so because a small error in the guessed value of R results in a smaller error in the calculated ΔN_p (i.e., the error is dampened out). In Tarner’s method, the opposite is true — a small error in ΔN_p results in a larger error in ΔG_p.

Muskat Method

Muskat’s method is different from Tarner’s and Tracy’s in that it does not require a trial and error procedure. However, it requires that one take the derivatives of various parameters. These are represented by differences. Thus, the pressure must be taken in small intervals for the Muskat representation to be acceptable. Because of this, the Muskat method is best suited for computers.

Basically, the Muskat method calculates the produced gas-oil ratio by two methods, which are

$R=\dfrac{k_{g}\, \mu _{o}\, B_{o}}{k_{o}\, \mu _{g}\, B_{g}}+R_{s}$ and $R=\dfrac{q_{g}}{q_{o}}$

where q_g and q_o are respectively the rates of gas and oil production in surface volumes. However, q_g and q_o indicate the rates of change with respect to time of the gas and oil in the reservoir. In equation form,

$q_{o}=\dfrac{\mathrm{d} }{\mathrm{d} t}\left ( \dfrac{S_{o}}{B_{o}} \right )$

and

$q_{g}=\dfrac{\mathrm{d} }{\mathrm{d} t}\left ( \dfrac{R_{s}S_{o}}{B_{o}}+\dfrac{\left ( 1-S_{o}-S_{wi} \right )}{B_{g}} \right )$

The two terms on the right-hand side of the q_gequation represent the gas in solution and the gas saturation. Since

$\dfrac{\mathrm{d} }{\mathrm{d} t}=\dfrac{\mathrm{d} }{\mathrm{d} p}\dfrac{\mathrm{d} p}{\mathrm{d} t}\cong \dfrac{\Delta }{\Delta p}\dfrac{\Delta p}{\Delta t}$

we can write

$R=\dfrac{q_{g}}{q_{o}}=\dfrac{\dfrac{\Delta }{\Delta p}\left ( \dfrac{R_{s}S_{o}}{B_{o}}+\dfrac{S_{g}}{B_{g}} \right )}{\dfrac{\Delta }{\Delta p}\left ( \dfrac{S_{o}}{B_{o}} \right )}$

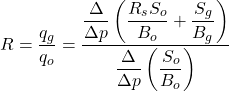
Expanding and solving for $\dfrac{\Delta S_{o}}{\Delta p}$ gives

$\dfrac{\Delta S_{o}}{\Delta p} = \dfrac{S_{o}\dfrac{\Delta }{\Delta p}\left ( \dfrac{R_{s}}{B_{o}} \right )+S_{g}\dfrac{\Delta }{\Delta p}\left ( \dfrac{1}{B_{g}} \right ) - R\, S_{o}\dfrac{\Delta }{\Delta p}\left ( \dfrac{1}{B_{o}} \right )}{\dfrac{R}{B_{o}}-\dfrac{R_{s}}{B_{o}}+\dfrac{1}{B_{g}}}$

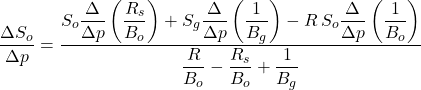
where R is

$R = \dfrac{k_{g}\, \mu _{o}\, B_{o}}{k_{o}\, \mu _{g}\, B_{g}} + R_{s}$

Thus, the incremental change in the oil saturation ΔS_o due to an incremental pressure decline Δp is calculated. The calculations proceed incrementally until an abandonment pressure is reached. Total oil recovery N_p is

$N_{p}=V_{p}\left ( \dfrac{S_{oi}}{B_{oi}}-\dfrac{S_{o}}{B_{o}} \right )$

where:

V_p= the pore volume in barrels

S_oi= initial oil saturation

S_o= oil saturation at abandonment pressure =S_oi−ΔS_o

Recovery Factor

Recovery by solution gas drive, as indicated previously, depends on the PVT properties and the efficiency of gas utilization in the reservoir to provide the driving energy. Recovery under the best conditions seldom exceeds 30%. When conditions are not favorable, such as for relatively viscous oil, or highly heterogeneous reservoirs, or both, recovery could be below 10%. As a rule of thumb one thinks of recovery around 15% for solution gas reservoirs.

A Case History of a Solution Gas Drive Reservoir

A good example of a solution gas drive reservoir is the Gloyd-Mitchell zone of the Rodessa field, located in Louisiana. (This resume is based on Craft and Hawkins [1959].) It is a flat reservoir that produces an oil of 42.8^º API gravity. The original bottomhole pressure was 2700 psig (18.6 MPa) with a solution gas-oil ratio of 627 $\tfrac{scf}{STB}$ (111.6 $\tfrac{m^3}{m^3}$ ). There was no indication of the presence of original gas, or an active water drive, in this zone.

After production of approximately 200,000 barrels (31,800 $\tfrac{m^3}{m^3}$ ) of oil, or just a few percent of the initial oil in place, the reservoir pressure dropped to the bubble-point pressure (2200 psig) (15.2 MPa). During this period of rapid decline of reservoir pressure, the GOR remained generally near R_si, which is an indication of the recovery by liquid expansion. As oil production continued, the reservoir pressure continued to fall. As soon as it reached the bubble-point pressure, a free gas phase developed. As this free gas expanded, the reservoir pressure drop slowed and the GOR stayed near the solution gas-oil ratio.

The oil production of this period was due to the expansion caused by a limited amount of free gas flow. As cumulative oil production reached approximately 3 million barrels (477,000 $m^3$ ), the gas began to flow more quickly than oil into the wells, since the gas saturation had reached the critical saturation. The gas-oil ratio increased at an ever-faster rate and reservoir gas was rapidly depleted. Many attempts were made to reduce the gas-oil ratio by shutting in the wells, by blanking of upper portions of the producing formation, and by perforating the lower parts, but all of them failed.