Mathematical Basin Analysis Models
Geodynamic and Thermal Models
Ungerer et al. (1984) estimate heat flow history based on models that provide quantitative predictions of subsidence and heat flow. Guidish et al. (1985) review several geodynamic models that predict the change in heat flow as a function of time, including those developed by Sleep (1971), McKenzie (1978), Falvey and Middleton (1981), and Royden et al. (1980). We can test the applicability of these geodynamic models to a given sedimentary basin by examining the differences between backstripped and predicted subsidence. We can also calibrate geodynamic models against measured thermal indicators, such as vitrinite reflectance (Lerche et al., 1984). We apply the heat flow history to determine the temperature history of rock units, and the subsequent maturation of source rocks.
Two of the geodynamic models we have discussed provide subsidence predictions compatible with observed subsidence. The McKenzie crustal stretching model (1978) (Figure 1, Evolution from a simple rift to a continental margin: [a] simple rifting model; [b] extension model; [c] continental margin model.)
for basin formation describes a rapid stretching of the continental lithosphere, accompanied by crustal thinning and passive upwelling of hot asthenosphere. The crust subsides through block faulting during this stage, which is followed by crustal cooling, thickening, and passive subsidence as thermal equilibrium is re-established. Royden et al. (1980) present equations for solving for various stretching factors, β. The stretching factor for “oceanization” of crust describes crust ranging from purely continental (β=0) to purely oceanic (β=1). Figure 2 (Extension and dike intrusion models: [a] theoretical surface elevation for an extensional margin),
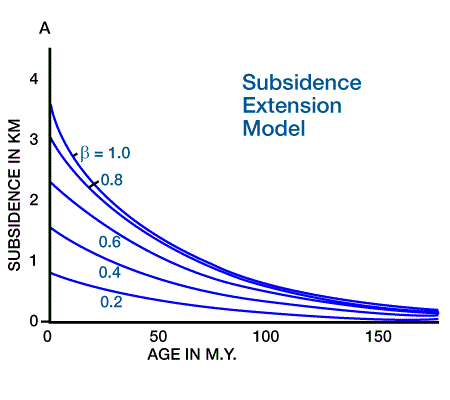
Figure 3 (Theoretical heat flow for an extensional margin),
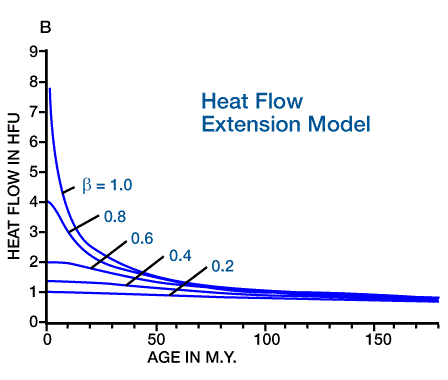
Figure 4 (Theoretical surface elevation for dike intrusion),
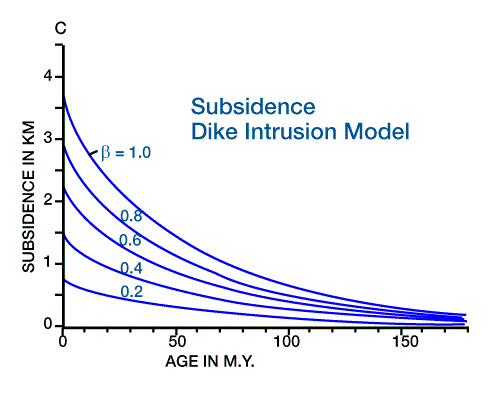
and Figure 5 (Theoretical heat flow for dike intrusion) plot solutions showing subsidence (a) and heat flow (b) over time for the McKenzie model.
One weakness of this model is its failure to include heat input from crustal radioactive decay. Sclater and Christie (1980) input an additional heat component in the calculations of McKenzie (1978) and Royden et al. (1980).
Royden et al. present a second model that produces results comparable to observed subsidence. This model proposes fracturing of continental crust and intrusion by dikes from the mantle (Figure 1 [b & c] ), with subsidence caused by replacing lighter crust with denser mantle material. Figure 2, Figure 3, Figure 4, and Figure 5. plots solutions for subsidence (c) and heat flow (d) over time for various stages of “oceanization” of the crust. Ungerer et al. (1984) also add heat produced by crustal radioactive heat decay to this model.
In order to apply these geodynamic models to predict heat flow histories, we must use the backstripping model to compensate for subsidence due to loading, and to reconstruct the subsidence history. Empirical measures of tectonic subsidence and age allow us to calculate a unique value of β, or to use the graphs shown in Figure 2 and Figure 4. Once we determine the value of β, we can calculate or measure heat flow histories from Figure 3 or Figure 4.
A comparison of the theoretical results shows that for end-member values of “oceanization” of crust (β=0 or β=1), heat flow histories predicted by these two models are similar. With intermediate values of b, early heat flow is higher for the dike-intrusion model. This result has implications for maturation histories, and consequently indicates the potential for using known maturation values to validate the choice of geodynamic models (Lerche et al., 1984).
Once we predict the heat flow history, we can apply thermal models to determine the time/temperature history for specific sedimentary units. Royden et al. (1980) point out that the temperature at depth is directly related to heat flow, so that we can determine the temperature at a given depth based on heat flow and thermal conductivity. Using the heat flow history and a simple model relating temperature to depth, we can determine the temperature history of each lithologic unit after estimating the thermal conductivity of the unit. Ungerer et al. (1984) developed a more comprehensive thermal model that factors in vertical heat transfer by conduction (convection and lateral heat transfer are not modeled). Their model also accounts for vertical heat transfer by expulsion of fluids during compaction, as well as variations in thermal properties of sediments with burial.
There are several models we can use to develop an understanding of the temperature history of a sedimentary basin. The input parameters for these models are both empirical and theoretical, and are based on numerous mathematical sub-models that predict such things as porosity, eustatic sea level changes, crustal response to loading, crustal thickness, heat transfer, and thermal properties of rocks. Our output from each of these models is only as reliable as the data we input.
