Lithology Identification From Well Logs

41 minutes read

Specialist Crossplots

Introduction

Crossplotting data from just two porosity well logs at any one time does not make full, simultaneous use of all the porosity data available when three porosity logs—density, neutron porosity and sonic or acoustic logs—have all been acquired. If a three-dimensional model could be built with the X, Y and Z axes corresponding to the neutron porosity, density and sonic log responses, then identifiable minerals would occupy unique points in the three-dimensional space. Complex, mixed lithology intervals, in particular, could thereby be more easily interpreted.

Specialist Crossplot Examples

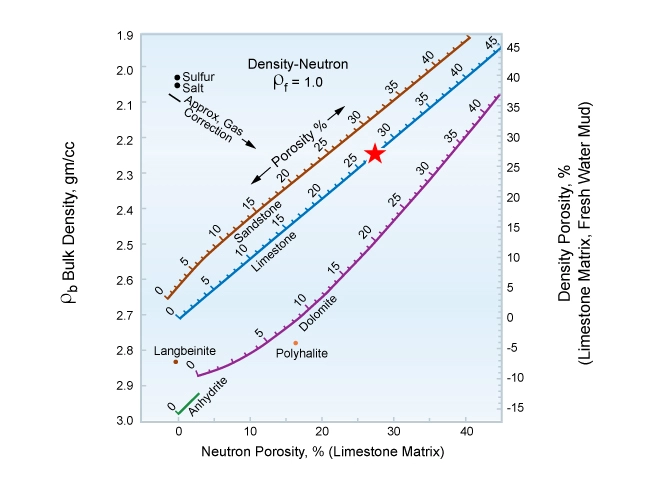
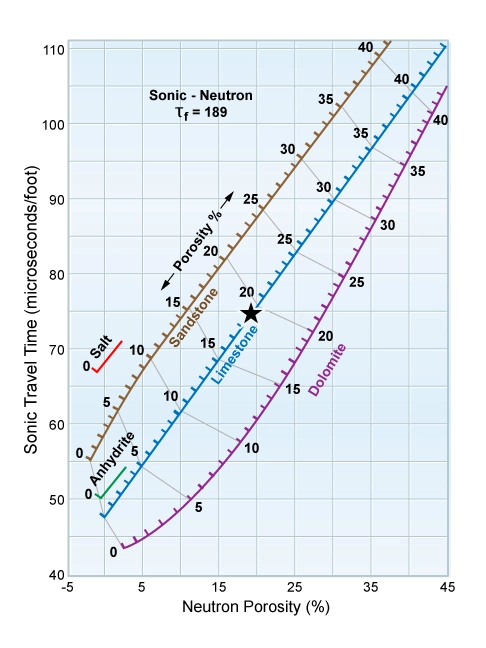
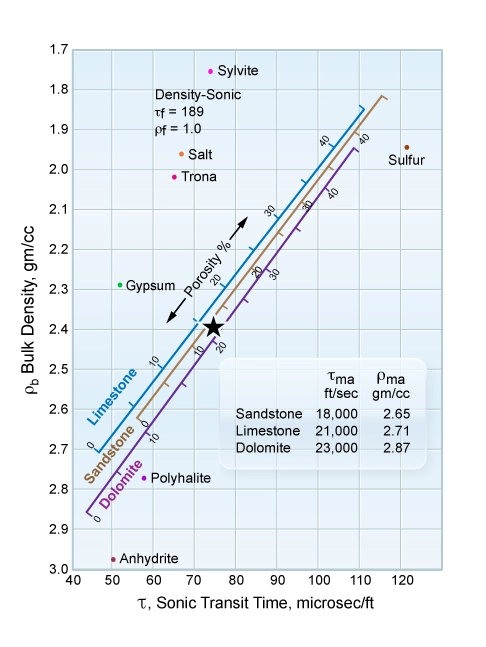
As an example, a 50% mixture of sandstone and dolomite would appear to be a limestone on both the neutron porosity versus density (Figure 1) and the neutron porosity versus sonic (Figure 2) crossplots. By contrast, the density versus sonic crossplot (Figure 3) would be more lithologically indicative for the formation.

A 50% sandstone and 50% dolomite mixture plots as a limestone on a neutron porosity versus density crossplot, lithology, lithology indicator, lithology determination from well logs, types of well logging, how to identify pine logs, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithological logs, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithological logs, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithological logs, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithological logs, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithological logs, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology identification, lithology logging, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithological logs, Rock type determination, Formation evaluation, Log interpretation, Well logging techniques, Well log analysis, Borehole geophysics, Geophysical logs, Wireline logging, Well log data, Lithologic characterization, Log-based lithology, Well log interpretation, Lithological identification, Formation lithology, Logging tools, Geologic interpretation, Logging parameters, Well log response, Sedimentary rocks identification, Reservoir characterization, Stratigraphic interpretation, Log-derived lithology, Rock properties estimation — **Figure 1**: A 50% sandstone and 50% dolomite mixture plots as a limestone on a neutron porosity versus density crossplot

A 50% sandstone and 50% dolomite mixture plots as a limestone on a neutron porosity versus sonic crossplot, lithology, lithology indicator, lithology determination from well logs, types of well logging, how to identify pine logs, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithological logs, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithological logs, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithological logs, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithological logs, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithological logs, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology identification, lithology logging, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithological logs, Rock type determination, Formation evaluation, Log interpretation, Well logging techniques, Well log analysis, Borehole geophysics, Geophysical logs, Wireline logging, Well log data, Lithologic characterization, Log-based lithology, Well log interpretation, Lithological identification, Formation lithology, Logging tools, Geologic interpretation, Logging parameters, Well log response, Sedimentary rocks identification, Reservoir characterization, Stratigraphic interpretation, Log-derived lithology, Rock properties estimation — **Figure 2**: A 50% sandstone and 50% dolomite mixture plots as a limestone on a neutron porosity versus sonic crossplot

50% sandstone and 50% dolomite mixture plots appropriately for its composition on a neutron porosity versus sonic crossplot, lithology indicator, lithology, lithology determination from well logs, types of well logging, how to identify pine logs, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithological logs, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithological logs, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithological logs, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithological logs, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithological logs, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology identification, lithology logging, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithological logs, Rock type determination, Formation evaluation, Log interpretation, Well logging techniques, Well log analysis, Borehole geophysics, Geophysical logs, Wireline logging, Well log data, Lithologic characterization, Log-based lithology, Well log interpretation, Lithological identification, Formation lithology, Logging tools, Geologic interpretation, Logging parameters, Well log response, Sedimentary rocks identification, Reservoir characterization, Stratigraphic interpretation, Log-derived lithology, Rock properties estimation — **Figure 3**: A 50% sandstone and 50% dolomite mixture plots appropriately for its composition on a neutron porosity versus sonic crossplot

M-N Plot

A number of techniques have been developed to resolve the problem of reducing three well log porosity readings to a two-dimensional crossplot. One of the early methods, still widely used, is the M-N plot. This crossplot requires that two parameters, M and N, be defined as:

$M = \dfrac{\Delta t_f - \Delta t}{\rho _b - \rho _f}\times 0.01$

$N = \dfrac{\phi _{N_{f}} - \phi _{N}}{\rho _b - \rho _f}$

Where ρ_f is fluid density. Note that ϕ_N needs to be in fractional units and that ϕ_N fluid is assumed to be 1.

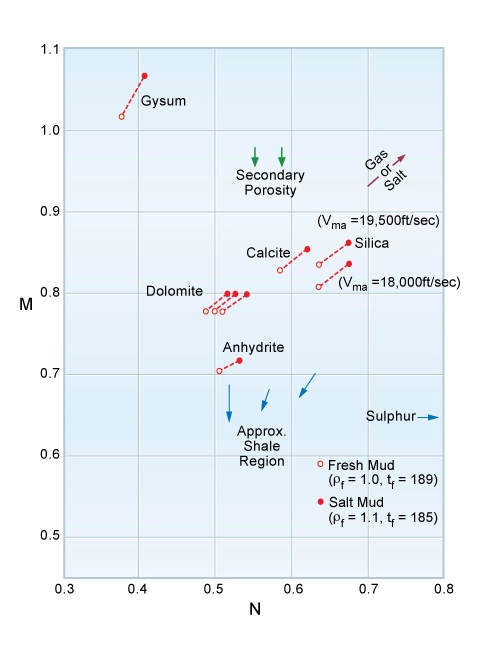
These two definitions are algebraic methods for finding the slope of a line that passes through a plotted point and the theoretical 100% porosity point. Since any pure conventional resource reservoir rock will plot on a line on the crossplots, and the slope of this line is substantially constant, that slope is a characteristic of a specific rock type. Having defined M and N and determined them for given depths logged in the well, the M and N pairs can be plotted on an M-N plot template (Figure 4).

M-N plot template, lithology, lithology indicator, lithology determination from well logs, types of well logging, how to identify pine logs, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithological logs, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithological logs, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithological logs, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithological logs, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithological logs, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology identification, lithology logging, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithological logs, Rock type determination, Formation evaluation, Log interpretation, Well logging techniques, Well log analysis, Borehole geophysics, Geophysical logs, Wireline logging, Well log data, Lithologic characterization, Log-based lithology, Well log interpretation, Lithological identification, Formation lithology, Logging tools, Geologic interpretation, Logging parameters, Well log response, Sedimentary rocks identification, Reservoir characterization, Stratigraphic interpretation, Log-derived lithology, Rock properties estimation — **Figure 4**: M-N plot template

However, the M-N plot has three relatively minor shortcomings:

It is not completely porosity independent for dolomite since the neutron porosity response is not exactly linear.
Each plotted data point depends somewhat on ρf, the fluid density.
The actual values of M and N for common minerals and reservoir rocks have no particular significance in themselves.

The M-N plot is still regularly used by petrophysicists. Figure 4 shows anhydrite and its hydrated form of gypsum identified from plotted M-N data.

However, some log analysts rely more on another crossplot technique that accomplishes the same end result of lithology identification but rather more elegantly, the MID plot.

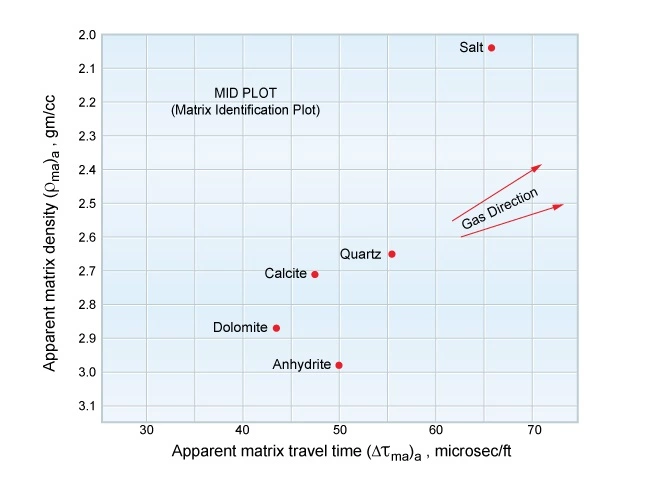
The Matrix Identification Plot (MID)

The matrix identification plot (MID) incorporates, in a single plot, all the three main porosity logs: density, neutron porosity and sonic. Its main advantages over the M-N plot include its independence from the formation porosity and the drilling mud type, and the benefit that it uses meaningful parameters directly related to rock properties that are more easily remembered.

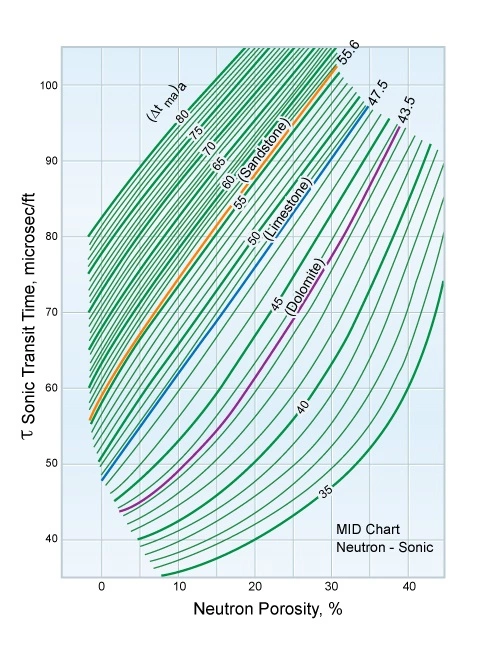
The neutron porosity and density logs are combined to define the apparent matrix density, (ρma)a. The neutron porosity and sonic logs are combined to define the apparent matrix travel time, (Δtma)a. These two parameters are then crossplotted to determine the formation lithology.

The value of (ρma)a is computed from the equations:

$\phi _X = \dfrac{\phi _{DLm} + \phi _{NLm} }{2}$

$(\phi _{ma})_{a} = \dfrac{\rho_B - \phi _X \cdot \rho _f}{1 - \phi _X}$

and likewise,

$(\Delta t_{ma})_a = \dfrac{\Delta t - \phi _X \cdot \Delta t_f}{1 - \phi _X}$

In practical log evaluation, these values are automatically computed within petrophysical analysis programs, or can be found from published charts.

MID Plots

Figure 5 defines (ρ_ma)_a for any ρ_b, ϕ_N pair.

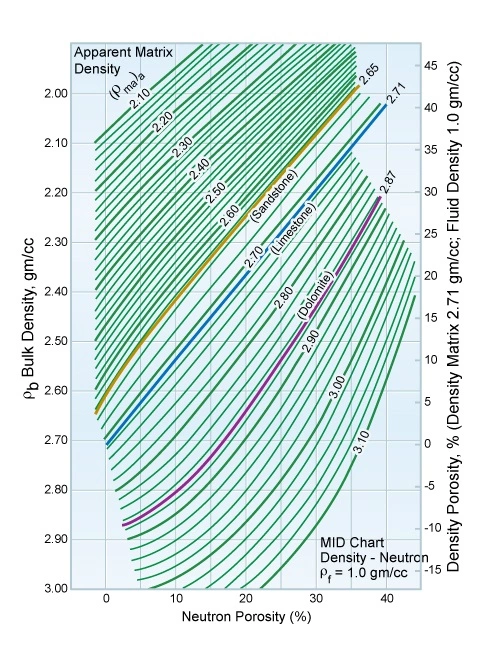
Apparent matrix density derived from the bulk density and neutron porosity for fresh water base muds, lithology, lithology indicator, lithology determination from well logs, types of well logging, how to identify pine logs, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithological logs, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithological logs, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithological logs, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithological logs, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithological logs, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology identification, lithology logging, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithological logs, Rock type determination, Formation evaluation, Log interpretation, Well logging techniques, Well log analysis, Borehole geophysics, Geophysical logs, Wireline logging, Well log data, Lithologic characterization, Log-based lithology, Well log interpretation, Lithological identification, Formation lithology, Logging tools, Geologic interpretation, Logging parameters, Well log response, Sedimentary rocks identification, Reservoir characterization, Stratigraphic interpretation, Log-derived lithology, Rock properties estimation — **Figure 5**: Apparent matrix density derived from the bulk density and neutron porosity for fresh water base muds

Figure 6 defines (Δt_ma)_a for any Δt, ϕ_N pair.

Apparent matrix travel time derived from neutron porosity and sonic transit time, lithology, lithology indicator, lithology determination from well logs, types of well logging, how to identify pine logs, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithological logs, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithological logs, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithological logs, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithological logs, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithological logs, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology identification, lithology logging, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithological logs, Rock type determination, Formation evaluation, Log interpretation, Well logging techniques, Well log analysis, Borehole geophysics, Geophysical logs, Wireline logging, Well log data, Lithologic characterization, Log-based lithology, Well log interpretation, Lithological identification, Formation lithology, Logging tools, Geologic interpretation, Logging parameters, Well log response, Sedimentary rocks identification, Reservoir characterization, Stratigraphic interpretation, Log-derived lithology, Rock properties estimation — **Figure 6**: Apparent matrix travel time derived from neutron porosity and sonic transit time

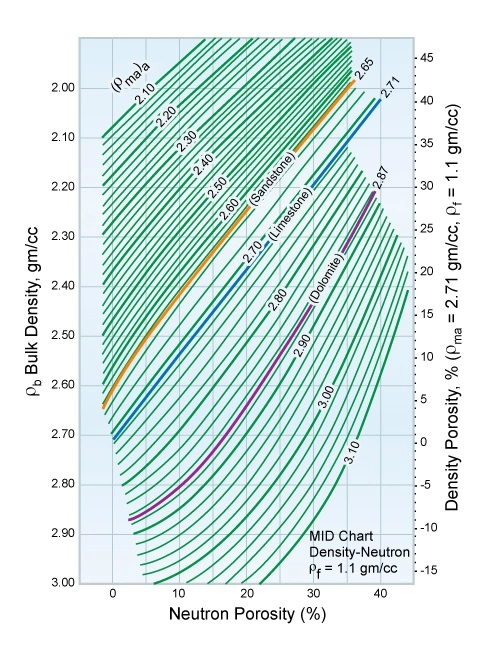
The computer algorithms shown in Figure 7 should be used in place of those in Figure 5 when ρ_f = 1.1 (salt water base mud filtrate).

Apparent matrix density derived from bulk density and neutron porosity for salt water base muds, lithology, lithology indicator, lithology determination from well logs, types of well logging, how to identify pine logs, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithological logs, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithological logs, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithological logs, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithological logs, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithological logs, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology identification, lithology logging, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithological logs, Rock type determination, Formation evaluation, Log interpretation, Well logging techniques, Well log analysis, Borehole geophysics, Geophysical logs, Wireline logging, Well log data, Lithologic characterization, Log-based lithology, Well log interpretation, Lithological identification, Formation lithology, Logging tools, Geologic interpretation, Logging parameters, Well log response, Sedimentary rocks identification, Reservoir characterization, Stratigraphic interpretation, Log-derived lithology, Rock properties estimation — **Figure 7**: Apparent matrix density derived from bulk density and neutron porosity for salt water base muds

Once (ρ_ma)_a and (Δ_ta)_a have been determined, they are crossplotted on the MID plot chart shown in Figure 8.

Matrix identification plot (MID) template, lithology, lithology indicator, lithology determination from well logs, types of well logging, how to identify pine logs, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithological logs, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithological logs, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithological logs, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithological logs, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithological logs, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology identification, lithology logging, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithology identification from well logs, lithology interpretation from logs, lithology logging, lithology identification, lithological logs, Rock type determination, Formation evaluation, Log interpretation, Well logging techniques, Well log analysis, Borehole geophysics, Geophysical logs, Wireline logging, Well log data, Lithologic characterization, Log-based lithology, Well log interpretation, Lithological identification, Formation lithology, Logging tools, Geologic interpretation, Logging parameters, Well log response, Sedimentary rocks identification, Reservoir characterization, Stratigraphic interpretation, Log-derived lithology, Rock properties estimation — **Figure 8**: Matrix identification plot (MID) template

When using either the MID plot or the M-N plot, it is useful to have a reference chart available which summarizes the values of ρma and Δtma, and log responses for common minerals and reservoir rocks. The Baker Hughes Atlas of Log Responses is one such reference Figure 9.