Geodynamic Models

32 minutes read

McKenzie Model Derivatives

The McKenzie model fails to predict first-order subsidence and heat flow in specific basins because the model invokes simple assumptions, such as finite, uniform extension with vertical, one-dimensional heat flow, that are inaccurate. Other geodynamic models have been derived from the McKenzie model for basins formed by stretching, to accommodate more complicated configurations and boundary conditions. These models accommodate non-instantaneous and non-uniform extension, two-dimensional (vertical and lateral) heat flow and flexural compensation of sediment and water loads. In this section, we focus on the geologic conditions where these derivative models are more applicable than the McKenzie model.

Jarvis and McKenzie (1980) analyzed the applicability of the assumption of instantaneous extension rates. Because conduction is an inefficient process for heat transfer, heat loss by conduction is negligible during rapid extension. So, the assumption of instantaneous extension is adequate for basins that rifted quickly. Slower extension rates allow more heat loss during extension and thus modify the timing of heat flow and thermal subsidence. If extension is slow enough all heat loss, and therefore all thermal subsidence, will occur during the extension phase. Because the total amount of subsidence depends on the amount of lithospheric thinning, the final magnitude of subsidence is constant and independent of the extension rate. By contrast, the timing and rates of thermal subsidence are dependent on the extension rate. Jarvis and McKenzie determined that we can apply the original McKenzie model if the following conditions are met:

$\Delta t <\dfrac {60}{\beta ^{2}}$ for $\beta \leq 2$ $\quad$ (1)

$\Delta t <60\left( 1-\dfrac {1}{\beta }\right) ^{2}$ for $\beta \geq 2$ $\quad$ (2)

where Δt is the duration of extension in millions of years. For example, for β = 2, we can apply the McKenzie model if the duration of extension is less than 15 My. If the conditions in Equations 1 and 2 are not met, then we must account for conduction during extension.

In some basins, the magnitude of initial subsidence, inferred from measured thicknesses of synrift sediments, is much less than that predicted by the McKenzie model, whose parameters are inferred from thermal subsidence or amount of crustal extension. This discrepancy implies a more buoyant post-extension lithosphere-asthenosphere than the McKenzie model assumes. One mechanism for increasing lithosphere-asthenosphere buoyancy, without changing the amount of crustal extension, is to thin the mantle lithosphere and the lower crust (i.e., the ductile portions of the lithosphere) more than the brittle upper crust (Sclater et al., 1980; Royden and Keen, 1980; Hellinger and Sclater, 1983). This differential tension allows the asthenosphere to rise farther than it would in the McKenzie model for the same degree of crustal extension, a configuration more similar to the qualitative extensional model shown in Figure 1.

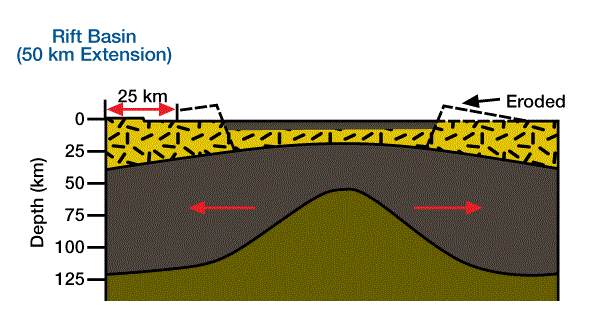
This differential tension allows the asthenosphere to rise farther than it would in the McKenzie model, Geodynamic Models — **FIGURE 1** This differential tension allows the asthenosphere to rise farther than it would in the McKenzie model

The mantle lithosphere is denser than the asthenosphere; as a result, thinning the mantle lid tends to cause uplift, whereas thinning the crust tends to cause subsidence.

Royden and Keen (1980) designed a two-layer extension model with a stretching factor β for the ductile lithosphere and $\gamma$ for the brittle lithosphere. The magnitude of initial subsidence depends on a balance between the amount of differential tension, and the degree to which asthenosphere replaces lithosphere. Buoyancy increases or decreases relative to the proportions of brittle and ductile layer thinning (Figure 2, Theoretical magnitude of initial subsidence or uplift from the two-layer, non-uniform extension model.

Theoretical magnitude of initial subsidence or uplift from the two-layer, non-uniform extension model, Geodynamic Models — **FIGURE 2** Theoretical magnitude of initial subsidence or uplift from the two-layer, non-uniform extension model

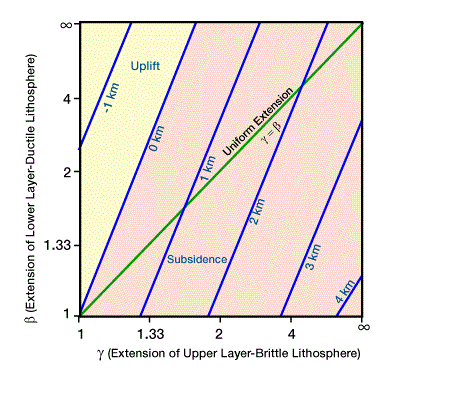
A stretching factor β is defined for the lower layer of ductile lithosphere, and a factor γ is defined for the upper layer of brittle lithosphere. For uniform extension of the McKenzie model, β= $\gamma$ . If the lower layer extends more than the upper layer [β> $\gamma$ ], the initial subsidence will be less than predicted by the uniform extension model.). As β increases relative to δ, the asthenosphere rises higher, adds more heat to the lithosphere, and increases the lithospheric-asthenospheric buoyancy. As a result, the magnitude of initial subsidence decreases or uplift is actually induced. Two-layer, depth-dependent stretching may explain synrift rift-flank uplift and erosion in positions of relatively thick crust, as illustrated in Figure 2, (A topographic bulge forms where mantle lithosphere is replaced with less dense viscous atmosphere; the flanks of the newly formed rift basin are eroded. Brittle crust and ductile asthenosphere are stretched and thinned.) (Hellinger and Sclater, 1980; Beaumont et al., 1982).

The assumption of one-dimensional vertical heat flow may be invalid for narrow extensional basins bounded on their flanks by cool crustal blocks acting as heat sinks. The lateral thermal gradients, in addition to the vertical thermal gradient, increases the rate of early heat loss. Modifications to basinal heat flow history alter the histories of temperature structure and thermal subsidence for a basin. Pitman and Andrews (1985) and Sawyer et al. (1985) found that stretching models using two-dimensional conductive heat flow more accurately predicted observed subsidence histories within narrow, pull-apart basins. (Pitman and Andrews defined a narrow basin as one whose width is less than lithospheric thickness.) They found that lateral conduction of heat increased the rate of cooling within a basin, and thus increased the subsidence rate early in the history of a basin relative to a one-dimensional cooling model.

A few workers have included flexural compensation of sediment and water loads, but not thermal loads, within stretching and cooling models (Watts and Steckler, 1981; Beaumont, Keen and Boutilier, 1982). By excluding thermal loads from flexural calculations, we implicitly assume that thermal loads are of sufficient magnitude that an Airy compensation model is adequate for the duration of cooling of the basin. Flexural compensation of surface loads results in a broader basin, creating successively more accommodation space landward of the stretched margin, and resulting in onlap of stratigraphic units (Figure 3).

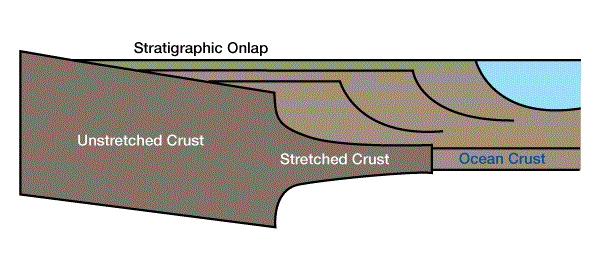
onlap of stratigraphic units, Geodynamic Models — **IGURE 3** Onlap of stratigraphic units

Watts and Steckler found that a McKenzie model adequately modeled the first-order shape of subsidence on the Atlantic margin in positions of thinned crust, but flexural compensation of surface loads provided a better match to gross stratigraphic relationships landward of thinned crust. Flexural compensation of fault controlled extension also results in “rebound” uplift, especially of the footwall.