Rheology and Subsidence Histories
We use rheological models to describe the temporal response of the lithosphere to forces and loads. Although there are numerous rheological models, linear elastic and viscoelastic models have been the most extensively applied. Both elastic and viscoelastic models predict a flexural response to a load, but they differ in their predictions of response history after a load is emplaced, and of rebound after the load is removed.
The linear elastic view assumes that the lithosphere behaves as an elastic solid so that deflections due to a load remain unchanged until the load is removed. Consequently, we can describe deflections of an elastic solid with a single value for flexural rigidity. Elastic models predict that when a load is removed the deflection will rebound to its initial shape, implying that no energy was dissipated through friction during loading and deflection. Jordan (1981) found that an elastic rheology is consistent with deflections due to thrust loading in the western United States.
We can modify this view by assuming that elastic thickness, h, and thus flexural rigidity, is defined by an isotherm (Figure 1, Four views of the layered structure of the earth, using different criteria for defining and recognizing layers.
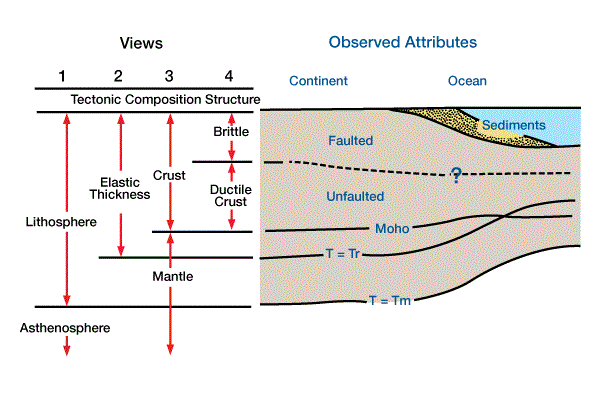
Views 1 and 2 use kinematic/tectonic criteria, with layers corresponding to isotherms. View 3 defines layers according to composition and/or density. View 4 uses structural response to stress as a criterion for defining layers.). Consequently, flexural rigidity varies with the thermal structure of the lithosphere. This model predicts that as the lithosphere ages, it cools and thickens, thereby increasing its flexural rigidity. Although flexural rigidity may vary with the thermal structure, the flexural response to a specific load can be described completely with the value of rigidity at the time of unloading.
Support for a modified elastic model has come primarily from investigations of loads on oceanic lithosphere. Estimations of elastic thicknesses from seamount, trench and spreading ridge loads on oceanic lithosphere have increased with lithospheric age (Figure 2, Plot of estimated thickness, h, versus age of oceanic lithosphere at the time of loading.

Elastic thicknesses were estimated by fitting a flexural compensation model to observed deflections due to loading. The solid lines are theoretical isotherms based ona cooling plate model. These data indicate that the temperature of relaxation, Tr is between 300 and 600 degrees C.) Although not well-established for continental lithosphere, this model has been used to infer age-dependent rigidities for passive margins (Keen, Beaumont and Boutilier, 1981; Watts, Karner and Steckler, 1982; Stockmal, Beaumont and Boutilier, 1986), and the Michigan Basin (Haxby, Turcotte and Bird, 1976). Karner and Watts (1982) showed that this model is consistent with free-air gravity anomalies on passive margins.
If flexural rigidity increases with age in the evolution of a basin, subsidence shape, and therefore basin shape, should progressively widen and become more shallow (Figure 3, Deflections of lithosphere with different flexural rigidities, due to the same load.
The load is 40 km wide, 1000 m high, and has a density of 2.5 gm/cm3. Subsidence is filled with water and the initial topography is horizontal.). For example, the broadening flexural response with age on a passive margin may account for the progressive onlap of sediments landward or the stretched continental lithosphere that has been observed on the Atlantic margin of the United States (Watts, Karner and Steckler, 1982). Foreland basins commonly involve compression and thrusting of previous passive margin sequences, and such basins may become broader and more shallow as thrusts are placed progressively landward onto older, cooler lithosphere (Stockmal, Beaumont and Boutilier, 1986).
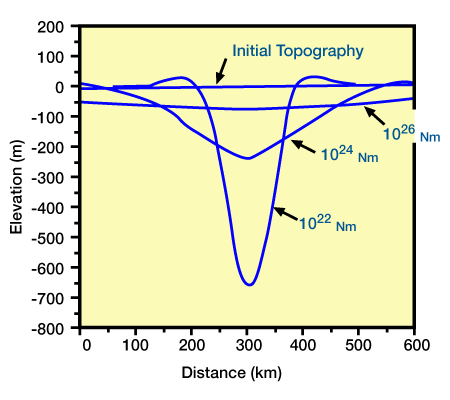
The second common view is that lithospheric rheology is viscoelastic. The behavior of a viscoelastic solid is transitional between an elastic solid and a viscous fluid. Elastic models assume that deflection due to a load is governed by a single value for rigidity. In contrast, viscoelastic models assume that after a load is emplaced, the lithosphere progressively softens, its rigidity decreases with time and the deflection approaches locally compensated isostatic equilibrium (Walcott, 1970; Beaumont, 1978) (Figure 4, Visoelastic response to a load.

With time, the lithosphere becomes more viscous and flexural rigidities decrease. Consequently, the load sinks, and the basin narrows and deepens.). Because deformation involves viscous flow, energy is lost to friction during deformation and the material will not return to its initial condition upon unloading.
We describe viscoelastic rheology using two parameters: the flexural rigidity, D, and a time constant describing the rate of decrease in flexural rigidity, t. Materials that have higher time constraints more nearly approach elastic solids and their rigidities decrease more slowly after load emplacement. Most flexural and Airy compensation models assume that deformation due to a load is instantaneous. Investigations of glacial rebound have shown that deformations actually occur viscoelastically with time constants of approximately 5,000 to 25,000 years (Walcott, 1970; Peltier, 1982).
Viscoelastic deformation with time constants of 1 My to more than 20 My is more applicable to understanding subsidence variations with basin spatial and temporal scales (Beaumont, 1978; Sleep and Snell, 1978, Beaumont, 1981; Nunn and Sleep, 1984). However, using this time constant, we cannot distinguish a viscoelastic response from an elastic response using only basin shapes because the viscoelastic response always has a flexural shape comparable to an elastic response. Because we need a history of deformation to test whether rheology is elastic or viscoelastic, stratigraphic data are most useful.
Histories of subsidence shapes within basins using the distribution and thicknesses of time-stratigraphic units has proven more consistent with a viscoelastic rheology in the Michigan (Sleep and Snell, 1976) and Alberta foreland basins (Beaumont, 1981). In contrast to sediment onlap and progressive basin widening with elastic rheology, viscoelastic rheologies predict a progressive basin narrowing and deepening because of the reduction of rigidity with time (Figure 4). Studies generally do not include an age-dependent initial rigidity with viscoelastic rheologies because thermal effects are believed to dominate viscoelastic effects for younger lithosphere (Beaumont, 1978; Stockmal, Beaumont and Boutilier, 1986).
Stratigraphic, gravity and bathymetric data within continental and oceanic basins are not consistent with either exclusively elastic or viscoelastic rheologies. The lithosphere cannot be purely viscoelastic because responses to all loads do not progress to complete isostatic compensation; the lithosphere can support some loads for hundreds of millions of years. But the lithosphere cannot be purely elastic because there are still deflections from loads that have been eroded for millions of years (e.g., Wachita and Appalachian foreland basins). This situation implies that there is loss of energy during loading leading to permanent deformation which is more consistent with a viscoelastic or plastic rheology. However, the data are consistent with temporal variations in rheology that are probably a function of load magnitudes and dimensions applied to a thermally controlled, rheologically layered earth.
Because load compensations have temporal variations, we cannot discern the load-response system within a basin solely from present basin shapes or gravity anomalies. If there are temporal variations in basin shapes, then — neglecting the effect of changes in eustasy — accommodation space for sediment accumulation will vary dynamically. Dynamic distribution of sediment loads modifies the tectonic subsidence shapes, further emphasizing temporal variations in subsidence response and influencing the final gravity anomaly and basin shape. For example, Karner and Watts (1982) calculated an effective lithospheric thickness from present bathymetric and free-air gravity data (Figure 2). The effective lithospheric thickness is less than we would expect from oceanic data and shows increasing thickness with age from thermal cooling. This condition is due to the fact that some of the sediments were deposited when the lithosphere was thinner, and their deflections have influenced the present bathymetry and gravity data. Consequently, detailed analysis of loads and responses for the purposes of understanding the dynamics of accommodation space, and thus stratigraphic architecture, requires us to integrate reconstructed time-stratigraphic data, as well as present basin shapes and gravity anomalies.
 Petro Shine The Place for Oil and Gas Professionals.
Petro Shine The Place for Oil and Gas Professionals.



